This article's lead section may be too long.(April 2014) |

Coalesced hashing, also called coalesced chaining, is a strategy of collision resolution in a hash table that forms a hybrid of separate chaining and open addressing.
This article's lead section may be too long.(April 2014) |

Coalesced hashing, also called coalesced chaining, is a strategy of collision resolution in a hash table that forms a hybrid of separate chaining and open addressing.
In a separate chaining hash table, items that hash to the same address are placed on a list (or "chain") at that address. This technique can result in a great deal of wasted memory because the table itself must be large enough to maintain a load factor that performs well (typically twice the expected number of items), and extra memory must be used for all but the first item in a chain (unless list headers are used, in which case extra memory must be used for all items in a chain).
Given a sequence "qrj," "aty," "qur," "dim," "ofu," "gcl," "rhv," "clq," "ecd," "qsu" of randomly generated three character long strings, the following table would be generated (using Bob Jenkins' One-at-a-Time hash algorithm) with a table of size 10:
| (null) | |||
| "clq" | |||
| "qur" | |||
| (null) | |||
| (null) | |||
| "dim" | |||
| "aty" | "qsu" | ||
| "rhv" | |||
| "qrj" | "ofu" | "gcl" | "ecd" |
| (null) |
This strategy is effective, efficient, and very easy to implement. However, sometimes the extra memory use might be prohibitive, and the most common alternative, open addressing, has uncomfortable disadvantages that decrease performance. The primary disadvantage of open addressing is primary and secondary clustering, in which searches may access long sequences of used buckets that contain items with different hash addresses; items with one hash address can thus lengthen searches for items with other hash addresses.
One solution to these issues is coalesced hashing. Coalesced hashing uses a similar technique as separate chaining, but instead of allocating new nodes for the linked list, buckets in the actual table are used. The first empty bucket in the table at the time of a collision is considered the collision bucket. When a collision occurs anywhere in the table, the item is placed in the collision bucket and a link is made between the chain and the collision bucket. It is possible for a newly inserted item to collide with items with a different hash address, such as the case in the example in the image when item "clq" is inserted. The chain for "clq" is said to "coalesce" with the chain of "qrj," hence the name of the algorithm. However, the extent of coalescing is minor compared with the clustering exhibited by open addressing. For example, when coalescing occurs, the length of the chain grows by only 1, whereas in open addressing, search sequences of arbitrary length may combine.
An important optimization, to reduce the effect of coalescing, is to restrict the address space of the hash function to only a subset of the table. For example, if the table has size M with buckets numbered from 0 to M − 1, we can restrict the address space so that the hash function only assigns addresses to the first N locations in the table. The remaining M − N buckets, called the cellar, are used exclusively for storing items that collide during insertion. No coalescing can occur until the cellar is exhausted.
The optimal choice of N relative to M depends upon the load factor (or fullness) of the table. A careful analysis shows that the value N = 0.86 × M yields near-optimum performance for most load factors. [1] [2]
Other variants for insertion are also possible that have improved search time. Deletion algorithms have been developed that preserve randomness, and thus the average search time analysis still holds after deletions. [1]
Insertion in C:
/* htab is the hash table, N is the size of the address space of the hash function, and M is the size of the entire table including the cellar. Collision buckets are allocated in decreasing order, starting with bucket M-1. */intinsert(charkey[]){unsignedh=hash(key,strlen(key))%N;if(htab[h]==NULL){/* Make a new chain */htab[h]=make_node(key,NULL);}else{structnode*it;intcursor=M-1;/* Find the first empty bucket */while(cursor>=0&&htab[cursor]!=NULL)--cursor;/* The table is full, terminate unsuccessfully */if(cursor==-1)return-1;htab[cursor]=make_node(key,NULL);/* Find the last node in the chain and point to it */it=htab[h];while(it->next!=NULL)it=it->next;it->next=htab[cursor];}return0;}One benefit of this strategy is that the search algorithm for separate chaining can be used without change in a coalesced hash table.
Lookup in C:
char*find(charkey[]){unsignedh=hash(key,strlen(key))%N;if(htab[h]!=NULL){structnode*it;/* Search the chain at index h */for(it=htab[h];it!=NULL;it=it->next){if(strcmp(key,it->data)==0)returnit->data;}}returnNULL;}Coalesced chaining avoids the effects of primary and secondary clustering, and as a result can take advantage of the efficient search algorithm for separate chaining. If the chains are short, this strategy is very efficient and can be highly condensed, memory-wise. As in open addressing, deletion from a coalesced hash table is awkward and potentially expensive, and resizing the table is terribly expensive and should be done rarely, if ever.[ citation needed ]

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.

A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable length output. The values returned by a hash function are called hash values, hash codes, hash digests, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.

In computing, a hash table, also known as a hash map or a hash set, is a data structure that implements an associative array, also called a dictionary, which is an abstract data type that maps keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
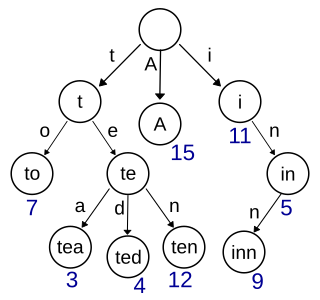
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.
In computer science, an associative array, map, symbol table, or dictionary is an abstract data type that stores a collection of pairs, such that each possible key appears at most once in the collection. In mathematical terms, an associative array is a function with finite domain. It supports 'lookup', 'remove', and 'insert' operations.

A distributed hash table (DHT) is a distributed system that provides a lookup service similar to a hash table. Key–value pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key. The main advantage of a DHT is that nodes can be added or removed with minimum work around re-distributing keys. Keys are unique identifiers which map to particular values, which in turn can be anything from addresses, to documents, to arbitrary data. Responsibility for maintaining the mapping from keys to values is distributed among the nodes, in such a way that a change in the set of participants causes a minimal amount of disruption. This allows a DHT to scale to extremely large numbers of nodes and to handle continual node arrivals, departures, and failures.

In computer science, a perfect hash functionh for a set S is a hash function that maps distinct elements in S to a set of m integers, with no collisions. In mathematical terms, it is an injective function.

In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r is a positive integer and a power x of 2, having x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

Linear probing is a scheme in computer programming for resolving collisions in hash tables, data structures for maintaining a collection of key–value pairs and looking up the value associated with a given key. It was invented in 1954 by Gene Amdahl, Elaine M. McGraw, and Arthur Samuel and first analyzed in 1963 by Donald Knuth.

Cuckoo hashing is a scheme in computer programming for resolving hash collisions of values of hash functions in a table, with worst-case constant lookup time. The name derives from the behavior of some species of cuckoo, where the cuckoo chick pushes the other eggs or young out of the nest when it hatches in a variation of the behavior referred to as brood parasitism; analogously, inserting a new key into a cuckoo hashing table may push an older key to a different location in the table.
2-choice hashing, also known as 2-choice chaining, is "a variant of a hash table in which keys are added by hashing with two hash functions. The key is put in the array position with the fewer (colliding) keys. Some collision resolution scheme is needed, unless keys are kept in buckets. The average-case cost of a successful search is , where is the number of keys and is the size of the array. The most collisions is with high probability."
Database tables and indexes may be stored on disk in one of a number of forms, including ordered/unordered flat files, ISAM, heap files, hash buckets, or B+ trees. Each form has its own particular advantages and disadvantages. The most commonly used forms are B-trees and ISAM. Such forms or structures are one aspect of the overall schema used by a database engine to store information.
In computer science, dynamic perfect hashing is a programming technique for resolving collisions in a hash table data structure. While more memory-intensive than its hash table counterparts, this technique is useful for situations where fast queries, insertions, and deletions must be made on a large set of elements.
In computer science, a search data structure is any data structure that allows the efficient retrieval of specific items from a set of items, such as a specific record from a database.

Hopscotch hashing is a scheme in computer programming for resolving hash collisions of values of hash functions in a table using open addressing. It is also well suited for implementing a concurrent hash table. Hopscotch hashing was introduced by Maurice Herlihy, Nir Shavit and Moran Tzafrir in 2008. The name is derived from the sequence of hops that characterize the table's insertion algorithm.
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.
The HAT-trie is a type of radix trie that uses array nodes to collect individual key–value pairs under radix nodes and hash buckets into an associative array. Unlike a simple hash table, HAT-tries store key–value in an ordered collection. The original inventors are Nikolas Askitis and Ranjan Sinha. Askitis & Zobel showed that building and accessing the HAT-trie key/value collection is considerably faster than other sorted access methods and is comparable to the array hash which is an unsorted collection. This is due to the cache-friendly nature of the data structure which attempts to group access to data in time and space into the 64 byte cache line size of the modern CPU.