
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In commutative algebra, the prime spectrum of a commutative ring R is the set of all prime ideals of R, and is usually denoted by ; in algebraic geometry it is simultaneously a topological space equipped with the sheaf of rings .
In mathematics, particularly linear algebra and functional analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized. This is extremely useful because computations involving a diagonalizable matrix can often be reduced to much simpler computations involving the corresponding diagonal matrix. The concept of diagonalization is relatively straightforward for operators on finite-dimensional vector spaces but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modeled by multiplication operators, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory for a historical perspective.
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
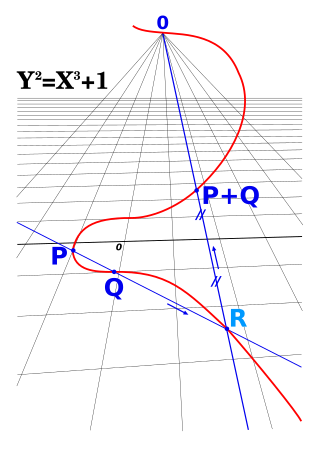
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing expander graphs.
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example is the subgroup of invertible 2 × 2 integer matrices of determinant 1 in which the off-diagonal entries are even. More generally, the notion of congruence subgroup can be defined for arithmetic subgroups of algebraic groups; that is, those for which we have a notion of 'integral structure' and can define reduction maps modulo an integer.
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with reference to a sheaf of rings that codifies this geometric information.
In abstract algebra, a representation of an associative algebra is a module for that algebra. Here an associative algebra is a ring. If the algebra is not unital, it may be made so in a standard way ; there is no essential difference between modules for the resulting unital ring, in which the identity acts by the identity mapping, and representations of the algebra.

In mathematics, a Lie algebra is semisimple if it is a direct sum of simple Lie algebras.
In algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties. The construction, while not functorial, is a fundamental tool in scheme theory.
In mathematical physics, the gamma matrices, also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin particles. Gamma matrices were introduced by Paul Dirac in 1928.
In mathematics, the Schur orthogonality relations, which were proven by Issai Schur through Schur's lemma, express a central fact about representations of finite groups. They admit a generalization to the case of compact groups in general, and in particular compact Lie groups, such as the rotation group SO(3).
Schur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups. It is named after two pioneers of representation theory of Lie groups, Issai Schur, who discovered the phenomenon, and Hermann Weyl, who popularized it in his books on quantum mechanics and classical groups as a way of classifying representations of unitary and general linear groups.
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
In abstract algebra, a cellular algebra is a finite-dimensional associative algebra A with a distinguished cellular basis which is particularly well-adapted to studying the representation theory of A.
In algebraic geometry, the Quot scheme is a scheme parametrizing sheaves on a projective scheme. More specifically, if X is a projective scheme over a Noetherian scheme S and if F is a coherent sheaf on X, then there is a scheme whose set of T-points is the set of isomorphism classes of the quotients of that are flat over T. The notion was introduced by Alexander Grothendieck.
In mathematics, a sheaf of O-modules or simply an O-module over a ringed space (X, O) is a sheaf F such that, for any open subset U of X, F(U) is an O(U)-module and the restriction maps F(U) → F(V) are compatible with the restriction maps O(U) → O(V): the restriction of fs is the restriction of f times the restriction of s for any f in O(U) and s in F(U).
Arithmetic Fuchsian groups are a special class of Fuchsian groups constructed using orders in quaternion algebras. They are particular instances of arithmetic groups. The prototypical example of an arithmetic Fuchsian group is the modular group . They, and the hyperbolic surface associated to their action on the hyperbolic plane often exhibit particularly regular behaviour among Fuchsian groups and hyperbolic surfaces.
This is a glossary of representation theory in mathematics.








































