
A machine is a physical system that uses power to apply forces and control movement to perform an action. The term is commonly applied to artificial devices, such as those employing engines or motors, but also to natural biological macromolecules, such as molecular machines. Machines can be driven by animals and people, by natural forces such as wind and water, and by chemical, thermal, or electrical power, and include a system of mechanisms that shape the actuator input to achieve a specific application of output forces and movement. They can also include computers and sensors that monitor performance and plan movement, often called mechanical systems.

An industrial robot is a robot system used for manufacturing. Industrial robots are automated, programmable and capable of movement on three or more axes.
DH, Dh, dh, or dH may refer to:

In computer animation and robotics, inverse kinematics is the mathematical process of calculating the variable joint parameters needed to place the end of a kinematic chain, such as a robot manipulator or animation character's skeleton, in a given position and orientation relative to the start of the chain. Given joint parameters, the position and orientation of the chain's end, e.g. the hand of the character or robot, can typically be calculated directly using multiple applications of trigonometric formulas, a process known as forward kinematics. However, the reverse operation is, in general, much more challenging.

A Cartesian coordinate robot is an industrial robot whose three principal axes of control are linear and are at right angles to each other. The three sliding joints correspond to moving the wrist up-down, in-out, back-forth. Among other advantages, this mechanical arrangement simplifies the robot control arm solution. It has high reliability and precision when operating in three-dimensional space. As a robot coordinate system, it is also effective for horizontal travel and for stacking bins.

In robotics, robot kinematics applies geometry to the study of the movement of multi-degree of freedom kinematic chains that form the structure of robotic systems. The emphasis on geometry means that the links of the robot are modeled as rigid bodies and its joints are assumed to provide pure rotation or translation.

FANUC is a Japanese group of companies that provide automation products and services such as robotics and computer numerical control wireless systems. These companies are principally FANUC Corporation of Japan, Fanuc America Corporation of Rochester Hills, Michigan, USA, and FANUC Europe Corporation S.A. of Luxembourg.
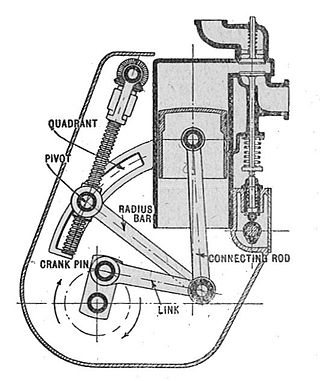
A mechanical linkage is an assembly of systems connected so as to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain.

Six degrees of freedom (6DOF), or sometimes six degrees of movement, refers to the six mechanical degrees of freedom of movement of a rigid body in three-dimensional space. Specifically, the body is free to change position as forward/backward (surge), up/down (heave), left/right (sway) translation in three perpendicular axes, combined with changes in orientation through rotation about three perpendicular axes, often termed yaw, pitch, and roll.

Serial manipulators are the most common industrial robots and they are designed as a series of links connected by motor-actuated joints that extend from a base to an end-effector. Often they have an anthropomorphic arm structure described as having a "shoulder", an "elbow", and a "wrist".

In robot kinematics, forward kinematics refers to the use of the kinematic equations of a robot to compute the position of the end-effector from specified values for the joint parameters.
In classical mechanics, a kinematic pair is a connection between two physical objects that imposes constraints on their relative movement (kinematics). German engineer Franz Reuleaux introduced the kinematic pair as a new approach to the study of machines that provided an advance over the notion of elements consisting of simple machines.

In mechanical engineering, a kinematic chain is an assembly of rigid bodies connected by joints to provide constrained motion that is the mathematical model for a mechanical system. As the word chain suggests, the rigid bodies, or links, are constrained by their connections to other links. An example is the simple open chain formed by links connected in series, like the usual chain, which is the kinematic model for a typical robot manipulator.
Line representations in robotics are used for the following:

In mechatronics engineering, the Denavit–Hartenberg parameters are the four parameters associated with the DH convention for attaching reference frames to the links of a spatial kinematic chain, or robot manipulator.

In engineering, a mechanism is a device that transforms input forces and movement into a desired set of output forces and movement. Mechanisms generally consist of moving components which may include Gears and gear trains; Belts and chain drives; cams and followers; Linkages; Friction devices, such as brakes or clutches; Structural components such as a frame, fasteners, bearings, springs, or lubricants; Various machine elements, such as splines, pins, or keys.
Kinematics equations are the constraint equations of a mechanical system such as a robot manipulator that define how input movement at one or more joints specifies the configuration of the device, in order to achieve a task position or end-effector location. Kinematics equations are used to analyze and design articulated systems ranging from four-bar linkages to serial and parallel robots.
The Robotics Toolbox is MATLAB toolbox software that supports research and teaching into arm-type and mobile robotics. While the Robotics Toolbox is free software, it requires the proprietary MATLAB environment in order to execute. The Toolbox forms the basis of the exercises in several textbooks.
The product of exponentials (POE) method is a robotics convention for mapping the links of a spatial kinematic chain. It is an alternative to Denavit–Hartenberg parameterization. While the latter method uses the minimal number of parameters to represent joint motions, the former method has a number of advantages: uniform treatment of prismatic and revolute joints, definition of only two reference frames, and an easy geometric interpretation from the use of screw axes for each joint.
In mechanical engineering, kinematic synthesis determines the size and configuration of mechanisms that shape the flow of power through a mechanical system, or machine, to achieve a desired performance. The word synthesis refers to combining parts to form a whole. Hartenberg and Denavit describe kinematic synthesis as
...it is design, the creation of something new. Kinematically, it is the conversion of a motion idea into hardware.













