In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.
Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative.

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or in terms of two positive parameters, denoted by alpha (α) and beta (β), that appear as exponents of the variable and its complement to 1, respectively, and control the shape of the distribution.

In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter k and a scale parameter θ
- With a shape parameter and an inverse scale parameter , called a rate parameter.
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions.
In combinatorics, the symbolic method is a technique for counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions. The method is mostly associated with Philippe Flajolet and is detailed in Part A of his book with Robert Sedgewick, Analytic Combinatorics, while the rest of the book explains how to use complex analysis in order to get asymptotic and probabilistic results on the corresponding generating functions.
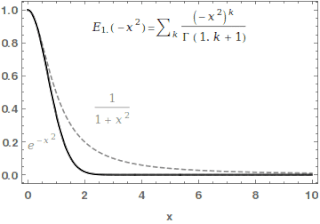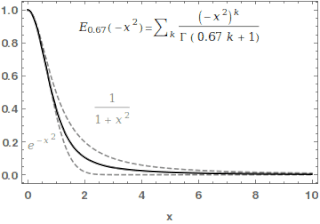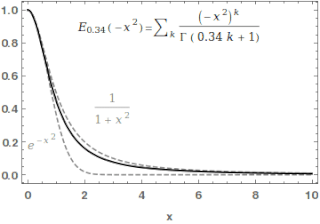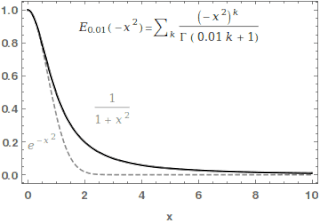
In mathematics, the Mittag-Leffler function is a special function, a complex function which depends on two complex parameters and . It may be defined by the following series when the real part of is strictly positive:
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class, then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.
In the field of mathematical analysis for the calculus of variations, Γ-convergence (Gamma-convergence) is a notion of convergence for functionals. It was introduced by Ennio De Giorgi.
In mathematics, the Kolmogorov continuity theorem is a theorem that guarantees that a stochastic process that satisfies certain constraints on the moments of its increments will be continuous. It is credited to the Soviet mathematician Andrey Nikolaevich Kolmogorov.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
An -superprocess, , within mathematics probability theory is a stochastic process on that is usually constructed as a special limit of near-critical branching diffusions.
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product is a product distribution.
Input-to-state stability (ISS) is a stability notion widely used to study stability of nonlinear control systems with external inputs. Roughly speaking, a control system is ISS if it is globally asymptotically stable in the absence of external inputs and if its trajectories are bounded by a function of the size of the input for all sufficiently large times. The importance of ISS is due to the fact that the concept has bridged the gap between input–output and state-space methods, widely used within the control systems community.
In mathematics and physics, Lieb–Thirring inequalities provide an upper bound on the sums of powers of the negative eigenvalues of a Schrödinger operator in terms of integrals of the potential. They are named after E. H. Lieb and W. E. Thirring.
Martin Hairer's theory of regularity structures provides a framework for studying a large class of subcritical parabolic stochastic partial differential equations arising from quantum field theory. The framework covers the Kardar–Parisi–Zhang equation, the equation and the parabolic Anderson model, all of which require renormalization in order to have a well-defined notion of solution.
In representation theory of mathematics, the Waldspurger formula relates the special values of two L-functions of two related admissible irreducible representations. Let k be the base field, f be an automorphic form over k, π be the representation associated via the Jacquet–Langlands correspondence with f. Goro Shimura (1976) proved this formula, when and f is a cusp form; Günter Harder made the same discovery at the same time in an unpublished paper. Marie-France Vignéras (1980) proved this formula, when and f is a newform. Jean-Loup Waldspurger, for whom the formula is named, reproved and generalized the result of Vignéras in 1985 via a totally different method which was widely used thereafter by mathematicians to prove similar formulas.
The convolutional sparse coding paradigm is an extension of the global sparse coding model, in which a redundant dictionary is modeled as a concatenation of circulant matrices. While the global sparsity constraint describes signal as a linear combination of a few atoms in the redundant dictionary , usually expressed as for a sparse vector , the alternative dictionary structure adopted by the convolutional sparse coding model allows the sparsity prior to be applied locally instead of globally: independent patches of are generated by "local" dictionaries operating over stripes of .
In mathematical analysis, the spaces of test functions and distributions are topological vector spaces (TVSs) that are used in the definition and application of distributions. Test functions are usually infinitely differentiable complex-valued functions on a non-empty open subset that have compact support. The space of all test functions, denoted by is endowed with a certain topology, called the canonical LF-topology, that makes into a complete Hausdorff locally convex TVS. The strong dual space of is called the space of distributions on and is denoted by where the "" subscript indicates that the continuous dual space of denoted by is endowed with the strong dual topology.
In probability theory and statistics, the modified half-normal distribution (MHN) is a three-parameter family of continuous probability distributions supported on the positive part of the real line. It can be viewed as a generalization of multiple families, including the half-normal distribution, truncated normal distribution, gamma distribution, and square root of the gamma distribution, all of which are special cases of the MHN distribution. Therefore, it is a flexible probability model for analyzing real-valued positive data. The name of the distribution is motivated by the similarities of its density function with that of the half-normal distribution.




















