Related Research Articles

Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a tornado in Brazil.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

A machine is a physical system using power to apply forces and control movement to perform an action. The term is commonly applied to artificial devices, such as those employing engines or motors, but also to natural biological macromolecules, such as molecular machines. Machines can be driven by animals and people, by natural forces such as wind and water, and by chemical, thermal, or electrical power, and include a system of mechanisms that shape the actuator input to achieve a specific application of output forces and movement. They can also include computers and sensors that monitor performance and plan movement, often called mechanical systems.
Group dynamics is a system of behaviors and psychological processes occurring within a social group, or between social groups. The study of group dynamics can be useful in understanding decision-making behaviour, tracking the spread of diseases in society, creating effective therapy techniques, and following the emergence and popularity of new ideas and technologies. These applications of the field are studied in psychology, sociology, anthropology, political science, epidemiology, education, social work, leadership studies, business and managerial studies, as well as communication studies.

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynamical system under a particular set of initial conditions, as the system evolves. As a phase space trajectory is uniquely determined for any given set of phase space coordinates, it is not possible for different orbits to intersect in phase space, therefore the set of all orbits of a dynamical system is a partition of the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems.

Alan David Sokal is an American professor of mathematics at University College London and professor emeritus of physics at New York University. He works in statistical mechanics and combinatorics. He is a critic of postmodernism, and caused the Sokal affair in 1996 when his deliberately nonsensical paper was published by Duke University Press's Social Text. He also co-authored a paper criticizing the critical positivity ratio concept in positive psychology.
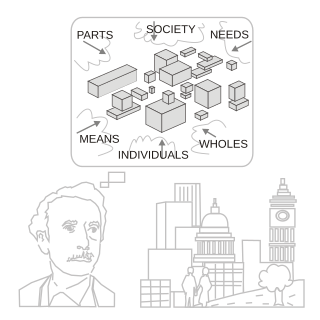
Systems science, also referred to as systems research, or, simply, systems, is a transdisciplinary field concerned with understanding systems—from simple to complex—in nature, society, cognition, engineering, technology and science itself. The field is diverse, spanning the formal, natural, social, and applied sciences.

A dynamical billiard is a dynamical system in which a particle alternates between free motion and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed. Billiards are Hamiltonian idealizations of the game of billiards, but where the region contained by the boundary can have shapes other than rectangular and even be multidimensional. Dynamical billiards may also be studied on non-Euclidean geometries; indeed, the first studies of billiards established their ergodic motion on surfaces of constant negative curvature. The study of billiards which are kept out of a region, rather than being kept in a region, is known as outer billiard theory.
The critical positivity ratio is a largely discredited concept in positive psychology positing an exact ratio of positive to negative emotions which distinguishes "flourishing" people from "languishing" people. The ratio was proposed by psychologists Barbara Fredrickson and Marcial Losada, who believed that they had identified an experimental measure of affect whose model-derived positive-to-negative ratio of 2.9013 defined a critical separation between flourishing and languishing individuals, as reported in their 2005 paper in American Psychologist. This concept of a critical positivity ratio was widely embraced by academic psychologists and the lay public; Fredrickson and Losada's paper had been cited more than 320 times by January 2014, and Fredrickson wrote a popular book expounding the concept of "the 3-to-1 ratio that will change your life". In it she wrote, "just as zero degrees Celsius is a special number in thermodynamics, the 3-to-1 positivity ratio may well be a magic number in human psychology." That sentence may be confusing zero degrees Celsius with zero degrees Kelvin. The latter is used to define a system with zero Entropy according to the Third law of thermodynamics.
Meta-learning is a branch of metacognition concerned with learning about one's own learning and learning processes.
The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey, with significant extensions by David Cass and Tjalling Koopmans. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, namely that several different initial chaotic conditions evolve in phase space in a way that never repeats, so all chaos is unpredictable. This underscores that chaotic systems can be completely deterministic and yet still be inherently unpredictable over long periods of time. Because chaos continually increases in systems, we cannot predict the future of systems well. E.g., even the small flap of a butterfly’s wings could set the world on a vastly different trajectory, such as by causing a hurricane. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.

Barbara Lee Fredrickson is an American professor in the department of psychology at the University of North Carolina at Chapel Hill, where she is the Kenan Distinguished Professor of Psychology. She is also the Principal Investigator of the Positive Emotions and Psychophysiology Lab (PEPLab) at the University of North Carolina at Chapel Hill.

A Boolean network consists of a discrete set of boolean variables each of which has a Boolean function assigned to it which takes inputs from a subset of those variables and output that determines the state of the variable it is assigned to. This set of functions in effect determines a topology (connectivity) on the set of variables, which then become nodes in a network. Usually, the dynamics of the system is taken as a discrete time series where the state of the entire network at time t+1 is determined by evaluating each variable's function on the state of the network at time t. This may be done synchronously or asynchronously.
Marcial Losada (1939–2020) was a Chilean psychologist, consultant, and former director of the Center for Advanced Research (CFAR) in Ann Arbor, Michigan. He is known for his work in academia and business focusing on the development of "high performance teams", and having participated in partially retracted collaborative work with Barbara Fredrickson of the University of North Carolina, a retraction for which he has been assigned the culpability.
The goal of most research on group development is to learn why and how small groups change over time. To quality of the output produced by a group, the type and frequency of its activities, its cohesiveness, the existence of group conflict.

Undulatory locomotion is the type of motion characterized by wave-like movement patterns that act to propel an animal forward. Examples of this type of gait include crawling in snakes, or swimming in the lamprey. Although this is typically the type of gait utilized by limbless animals, some creatures with limbs, such as the salamander, forgo use of their legs in certain environments and exhibit undulatory locomotion. In robotics this movement strategy is studied in order to create novel robotic devices capable of traversing a variety of environments.

In mathematics, a strange nonchaotic attractor (SNA) is a form of attractor which, while converging to a limit, is strange, because it is not piecewise differentiable, and also non-chaotic, in that its Lyapunov exponents are non-positive. SNAs were introduced as a topic of study by Grebogi et al. in 1984. SNAs can be distinguished from periodic, quasiperiodic and chaotic attractors using the 0-1 test for chaos.
References
- 1 2 Losada, M. and Heaphy, E. (2004). "The role of positivity and connectivity in the performance of business teams: A nonlinear dynamics model", American Behavioral Scientist, 47 (6), pp. 740–765.
- ↑ "Ratio for a good life exposed as 'nonsense'". Science News . 12 August 2013. Archived from the original on 26 August 2013. Retrieved 15 August 2013.
- Brown, N. J. L., Sokal, A. D., & Friedman, H. L. (2013). "The complex dynamics of wishful thinking: the critical positivity ratio", American Psychologist, 68 (9), pp. 801-813 - ↑ Navas, A. (2011), "Un cas d'inconscience (?)", Images des Mathématiques(in French)