
In the theory of computational complexity, the travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

In mathematics, a monotonic function is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
A* is a graph traversal and pathfinding algorithm that is used in many fields of computer science due to its completeness, optimality, and optimal efficiency. Given a weighted graph, a source node and a goal node, the algorithm finds the shortest path from source to goal.
In computer science, iterative deepening search or more specifically iterative deepening depth-first search is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal. Since it visits all the nodes in the search tree down to depth before visiting any nodes at depth , the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
Decision tree learning is a supervised learning approach used in statistics, data mining and machine learning. In this formalism, a classification or regression decision tree is used as a predictive model to draw conclusions about a set of observations.
Iterative deepening A* (IDA*) is a graph traversal and path search algorithm that can find the shortest path between a designated start node and any member of a set of goal nodes in a weighted graph. It is a variant of iterative deepening depth-first search that borrows the idea to use a heuristic function to conservatively estimate the remaining cost to get to the goal from the A* search algorithm. Since it is a depth-first search algorithm, its memory usage is lower than in A*, but unlike ordinary iterative deepening search, it concentrates on exploring the most promising nodes and thus does not go to the same depth everywhere in the search tree. Unlike A*, IDA* does not utilize dynamic programming and therefore often ends up exploring the same nodes many times.
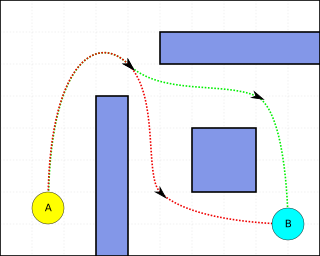
Pathfinding or pathing is the search, by a computer application, for the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.
Bidirectional search is a graph search algorithm that finds a shortest path from an initial vertex to a goal vertex in a directed graph. It runs two simultaneous searches: one forward from the initial state, and one backward from the goal, stopping when the two meet. The reason for this approach is that in many cases it is faster: for instance, in a simplified model of search problem complexity in which both searches expand a tree with branching factor b, and the distance from start to goal is d, each of the two searches has complexity O(bd/2) (in Big O notation), and the sum of these two search times is much less than the O(bd) complexity that would result from a single search from the beginning to the goal.
In mathematical optimization, the push–relabel algorithm is an algorithm for computing maximum flows in a flow network. The name "push–relabel" comes from the two basic operations used in the algorithm. Throughout its execution, the algorithm maintains a "preflow" and gradually converts it into a maximum flow by moving flow locally between neighboring nodes using push operations under the guidance of an admissible network maintained by relabel operations. In comparison, the Ford–Fulkerson algorithm performs global augmentations that send flow following paths from the source all the way to the sink.
In computational complexity theory, Polynomial Local Search (PLS) is a complexity class that models the difficulty of finding a locally optimal solution to an optimization problem. The main characteristics of problems that lie in PLS are that the cost of a solution can be calculated in polynomial time and the neighborhood of a solution can be searched in polynomial time. Therefore it is possible to verify whether or not a solution is a local optimum in polynomial time. Furthermore, depending on the problem and the algorithm that is used for solving the problem, it might be faster to find a local optimum instead of a global optimum.
In computer science, specifically in algorithms related to pathfinding, a heuristic function is said to be admissible if it never overestimates the cost of reaching the goal, i.e. the cost it estimates to reach the goal is not higher than the lowest possible cost from the current point in the path. In other words, it should act as a lower bound.
In mathematical optimization and computer science, heuristic is a technique designed for problem solving more quickly when classic methods are too slow for finding an exact or approximate solution, or when classic methods fail to find any exact solution in a search space. This is achieved by trading optimality, completeness, accuracy, or precision for speed. In a way, it can be considered a shortcut.
Capacitated minimum spanning tree is a minimal cost spanning tree of a graph that has a designated root node and satisfies the capacity constraint . The capacity constraint ensures that all subtrees incident on the root node have no more than nodes. If the tree nodes have weights, then the capacity constraint may be interpreted as follows: the sum of weights in any subtree should be no greater than . The edges connecting the subgraphs to the root node are called gates. Finding the optimal solution is NP-hard.
In computer science, the method of contraction hierarchies is a speed-up technique for finding the shortest-path in a graph. The most intuitive applications are car-navigation systems: a user wants to drive from to using the quickest possible route. The metric optimized here is the travel time. Intersections are represented by vertices, the road sections connecting them by edges. The edge weights represent the time it takes to drive along this segment of the road. A path from to is a sequence of edges ; the shortest path is the one with the minimal sum of edge weights among all possible paths. The shortest path in a graph can be computed using Dijkstra's algorithm but, given that road networks consist of tens of millions of vertices, this is impractical. Contraction hierarchies is a speed-up method optimized to exploit properties of graphs representing road networks. The speed-up is achieved by creating shortcuts in a preprocessing phase which are then used during a shortest-path query to skip over "unimportant" vertices. This is based on the observation that road networks are highly hierarchical. Some intersections, for example highway junctions, are "more important" and higher up in the hierarchy than for example a junction leading into a dead end. Shortcuts can be used to save the precomputed distance between two important junctions such that the algorithm doesn't have to consider the full path between these junctions at query time. Contraction hierarchies do not know about which roads humans consider "important", but they are provided with the graph as input and are able to assign importance to vertices using heuristics.
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic.
LPA* or Lifelong Planning A* is an incremental heuristic search algorithm based on A*. It was first described by Sven Koenig and Maxim Likhachev in 2001.



































