Constraint programming (CP) is a paradigm for solving combinatorial problems that draws on a wide range of techniques from artificial intelligence, computer science, and operations research. In constraint programming, users declaratively state the constraints on the feasible solutions for a set of decision variables. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties of a solution to be found. In addition to constraints, users also need to specify a method to solve these constraints. This typically draws upon standard methods like chronological backtracking and constraint propagation, but may use customized code like a problem-specific branching heuristic.
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, Boolean satisfiability problem (SAT), the satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.
Backtracking is a class of algorithms for finding solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution.
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.
In artificial intelligence and operations research, constraint satisfaction is the process of finding a solution through a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a set of values for the variables that satisfies all constraints—that is, a point in the feasible region.
In the domain of physics and probability, a Markov random field (MRF), Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. In other words, a random field is said to be a Markov random field if it satisfies Markov properties. The concept originates from the Sherrington–Kirkpatrick model.
In constraint satisfaction, local consistency conditions are properties of constraint satisfaction problems related to the consistency of subsets of variables or constraints. They can be used to reduce the search space and make the problem easier to solve. Various kinds of local consistency conditions are leveraged, including node consistency, arc consistency, and path consistency.
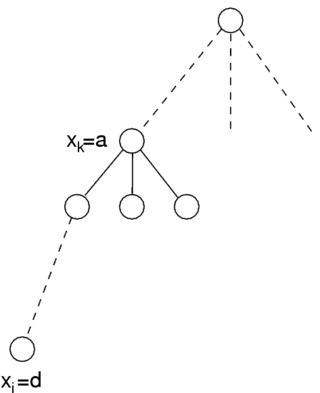
In constraint satisfaction, backmarking is a variant of the backtracking algorithm.
In backtracking algorithms, look ahead is the generic term for a subprocedure that attempts to foresee the effects of choosing a branching variable to evaluate one of its values. The two main aims of look-ahead are to choose a variable to evaluate next and the order of values to assign to it.

In backtracking algorithms, backjumping is a technique that reduces search space, therefore increasing efficiency. While backtracking always goes up one level in the search tree when all values for a variable have been tested, backjumping may go up more levels. In this article, a fixed order of evaluation of variables is used, but the same considerations apply to a dynamic order of evaluation.

In constraint satisfaction, local search is an incomplete method for finding a solution to a problem. It is based on iteratively improving an assignment of the variables until all constraints are satisfied. In particular, local search algorithms typically modify the value of a variable in an assignment at each step. The new assignment is close to the previous one in the space of assignment, hence the name local search.
In mathematical optimization, constrained optimization is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied.
Within artificial intelligence and operations research for constraint satisfaction a hybrid algorithm solves a constraint satisfaction problem by the combination of two different methods, for example variable conditioning and constraint inference
Constraint logic programming is a form of constraint programming, in which logic programming is extended to include concepts from constraint satisfaction. A constraint logic program is a logic program that contains constraints in the body of clauses. An example of a clause including a constraint is A(X,Y):-X+Y>0,B(X),C(Y). In this clause, X+Y>0 is a constraint; A(X,Y), B(X), and C(Y) are literals as in regular logic programming. This clause states one condition under which the statement A(X,Y) holds: X+Y is greater than zero and both B(X) and C(Y) are true.
Distributed constraint optimization is the distributed analogue to constraint optimization. A DCOP is a problem in which a group of agents must distributedly choose values for a set of variables such that the cost of a set of constraints over the variables is minimized.
The complexity of constraint satisfaction is the application of computational complexity theory on constraint satisfaction. It has mainly been studied for discriminating between tractable and intractable classes of constraint satisfaction problems on finite domains.
In computer science, conflict-driven clause learning (CDCL) is an algorithm for solving the Boolean satisfiability problem (SAT). Given a Boolean formula, the SAT problem asks for an assignment of variables so that the entire formula evaluates to true. The internal workings of CDCL SAT solvers were inspired by DPLL solvers. The main difference between CDCL and DPLL is that CDCL's back jumping is non-chronological.
In computer science, an interchangeability algorithm is a technique used to more efficiently solve constraint satisfaction problems (CSP). A CSP is a mathematical problem in which objects, represented by variables, are subject to constraints on the values of those variables; the goal in a CSP is to assign values to the variables that are consistent with the constraints. If two variables A and B in a CSP may be swapped for each other without changing the nature of the problem or its solutions, then A and B are interchangeable variables. Interchangeable variables represent a symmetry of the CSP and by exploiting that symmetry, the search space for solutions to a CSP problem may be reduced. For example, if solutions with A=1 and B=2 have been tried, then by interchange symmetry, solutions with B=1 and A=2 need not be investigated.
The Boolean satisfiability problem can be stated formally as: given a Boolean expression with variables, finding an assignment of the variables such that is true. It is seen as the canonical NP-complete problem. While no efficient algorithm is known to solve this problem in the general case, there are certain heuristics, informally called 'rules of thumb' in programming, that can usually help solve the problem reasonably efficiently.













