Definition
Let be a stochastic process in . The process is continuous in probability when converges in probability to whenever converges to . [2]
In probability theory, a stochastic process is said to be continuous in probability or stochastically continuous if its distributions converge whenever the values in the index set converge. [1] [2]
Let be a stochastic process in . The process is continuous in probability when converges in probability to whenever converges to . [2]
Feller processes are continuous in probability at . Continuity in probability is a sometimes used as one of the defining property for Lévy process. [1] Any process that is continuous in probability and has independent increments has a version that is càdlàg. [2] As a result, some authors immediately define Lévy process as being càdlàg and having independent increments. [3]
In probability theory, an elementary event, also called an atomic event or sample point, is an event which contains only a single outcome in the sample space. Using set theory terminology, an elementary event is a singleton. Elementary events and their corresponding outcomes are often written interchangeably for simplicity, as such an event corresponding to precisely one outcome.
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes, which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion. Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability theory describing such behaviour are the law of large numbers and the central limit theorem.

In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance.
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behavior can be characterized: two readily understood behaviors are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.

In mathematics, the Wiener process is a real valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.
In probability theory, independent increments are a property of stochastic processes and random measures. Most of the time, a process or random measure has independent increments by definition, which underlines their importance. Some of the stochastic processes that by definition possess independent increments are the Wiener process, all Lévy processes, all additive process and the Poisson point process.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

In probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”: a random variable whose value is interpreted as the time at which a given stochastic process exhibits a certain behavior of interest. A stopping time is often defined by a stopping rule, a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always lead to a decision to stop at some finite time.

Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and other martingales. Quadratic variation is just one kind of variation of a process.
In mathematics, the Cramér–Wold theorem in measure theory states that a Borel probability measure on is uniquely determined by the totality of its one-dimensional projections. It is used as a method for proving joint convergence results. The theorem is named after Harald Cramér and Herman Ole Andreas Wold.
Olav Kallenberg is a probability theorist known for his work on exchangeable stochastic processes and for his graduate-level textbooks and monographs. Kallenberg is a professor of mathematics at Auburn University in Alabama in the USA.
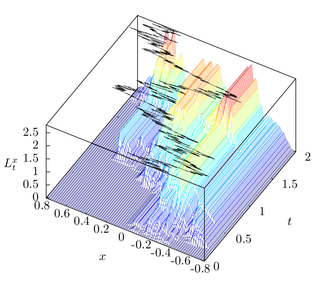
In the mathematical theory of stochastic processes, local time is a stochastic process associated with semimartingale processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level. Local time appears in various stochastic integration formulas, such as Tanaka's formula, if the integrand is not sufficiently smooth. It is also studied in statistical mechanics in the context of random fields.
In mathematics, progressive measurability is a property in the theory of stochastic processes. A progressively measurable process, while defined quite technically, is important because it implies the stopped process is measurable. Being progressively measurable is a strictly stronger property than the notion of being an adapted process. Progressively measurable processes are important in the theory of Itô integrals.
In the study of stochastic processes in mathematics, a hitting time is the first time at which a given process "hits" a given subset of the state space. Exit times and return times are also examples of hitting times.
In probability theory, a real valued stochastic process X is called a semimartingale if it can be decomposed as the sum of a local martingale and a càdlàg adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itô integral and the Stratonovich integral can be defined.
In probability theory, a probability distribution is infinitely divisible if it can be expressed as the probability distribution of the sum of an arbitrary number of independent and identically distributed (i.i.d.) random variables. The characteristic function of any infinitely divisible distribution is then called an infinitely divisible characteristic function.
In probability theory, a stochastic process is said to have stationary increments if its change only depends on the time span of observation, but not on the time when the observation was started. Many large families of stochastic processes have stationary increments either by definition or by construction
In mathematics, a càdlàg, RCLL, or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere. Càdlàg functions are important in the study of stochastic processes that admit jumps, unlike Brownian motion, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.
In probability theory, a Subordinator is a stochastic process that is non-negative and whose increments are stationary and independent. Subordinators are a special class of Lévy process that play an important role in the theory of local time. In this context, subordinators descibe the evolution of time within another stochastic process, the subordinated stochastic process. In other words, a subordinator will determine the random number of "time steps" that occur within the subordinated process for a given unit of chronological time.