Related Research Articles

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".

The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.
A New Kind of Science is a book by Stephen Wolfram, published by his company Wolfram Research under the imprint Wolfram Media in 2002. It contains an empirical and systematic study of computational systems such as cellular automata. Wolfram calls these systems simple programs and argues that the scientific philosophy and methods appropriate for the study of simple programs are relevant to other fields of science.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
An excitable medium is a nonlinear dynamical system which has the capacity to propagate a wave of some description, and which cannot support the passing of another wave until a certain amount of time has passed.
A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used instead of "hybrid system", to distinguish from other usages of "hybrid system", such as the combination neural nets and fuzzy logic, or of electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to test scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged.
A cellular automaton (CA) is Life-like if it meets the following criteria:
A continuous automaton can be described as a cellular automaton extended so that the valid states a cell can take are not just discrete, but continuous, for example, the real number range [0,1]. The cells however remain discretely separated from each other. One example is called computational verb cellular network (CVCN), of which the states of cells are in the region of [0,1].
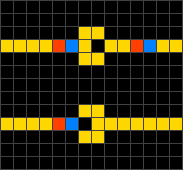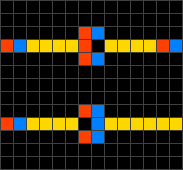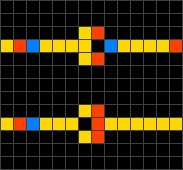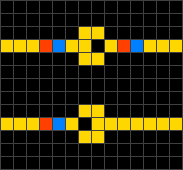
Wireworld, alternatively WireWorld, is a cellular automaton first proposed by Brian Silverman in 1987, as part of his program Phantom Fish Tank. It subsequently became more widely known as a result of an article in the "Computer Recreations" column of Scientific American. Wireworld is particularly suited to simulating transistors, and is Turing-complete.
In computer science and machine learning, cellular neural networks (CNN) or cellular nonlinear networks (CNN) are a parallel computing paradigm similar to neural networks, with the difference that communication is allowed between neighbouring units only. Typical applications include image processing, analyzing 3D surfaces, solving partial differential equations, reducing non-visual problems to geometric maps, modelling biological vision and other sensory-motor organs.

Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm", which will become the daughter loop. The "genes" instruct it to make three left turns, completing the loop, which then disconnects from its parent.
A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.
Hierarchical temporal memory (HTM) is a biologically constrained machine intelligence technology developed by Numenta. Originally described in the 2004 book On Intelligence by Jeff Hawkins with Sandra Blakeslee, HTM is primarily used today for anomaly detection in streaming data. The technology is based on neuroscience and the physiology and interaction of pyramidal neurons in the neocortex of the mammalian brain.
The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund credited Curtis and Lyndon as co-discoverers. It has been called "one of the fundamental results in symbolic dynamics".
The movable cellular automaton (MCA) method is a method in computational solid mechanics based on the discrete concept. It provides advantages both of classical cellular automaton and discrete element methods. One important advantage of the MCA method is that it permits direct simulation of material fracture, including damage generation, crack propagation, fragmentation, and mass mixing. It is difficult to simulate these processes by means of continuum mechanics methods, so some new concepts like peridynamics are required. Discrete element method is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. As the cell size of the automaton approaches zero, MCA behavior approaches classical continuum mechanics methods. The MCA method was developed in the group of S.G. Psakhie

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
The Greenberg–Hastings Cellular Automaton is a three state two dimensional cellular automaton named after James M. Greenberg and Stuart Hastings, designed to model excitable media, One advantage of a CA model is ease of computation. The model can be understood quite well using simple "hand" calculations, not involving a computer. Another advantage is that, at least in this case, one can prove a theorem characterizing those initial conditions which lead to repetitive behavior.
The spike response model (SRM) is a spiking neuron model in which spikes are generated by either a deterministic or a stochastic threshold process. In the SRM, the membrane voltage V is described as a linear sum of the postsynaptic potentials (PSPs) caused by spike arrivals to which the effects of refractoriness and adaptation are added. The threshold is either fixed or dynamic. In the latter case it increases after each spike. The SRM is flexible enough to account for a variety of neuronal firing pattern in response to step current input. The SRM has also been used in the theory of computation to quantify the capacity of spiking neural networks; and in the neurosciences to predict the subthreshold voltage and the firing times of cortical neurons during stimulation with a time-dependent current stimulation. The name Spike Response Model points to the property that the two important filters and of the model can be interpreted as the response of the membrane potential to an incoming spike (response kernel , the PSP) and to an outgoing spike (response kernel , also called refractory kernel). The SRM has been formulated in continuous time and in discrete time. The SRM can be viewed as a generalized linear model (GLM) or as an (integrated version of) a generalized integrate-and-fire model with adaptation.
References
- ↑ H. R. Wilson and J. D. Cowan. "Excitatory and inhibitory interactions in localized populations of model neurons" Biophysical Journal, 12:1–24, 1972.
- ↑ H. R. Wilson and J. D. Cowan. "A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue" Kybernetik, 13:55–80, 1973.
- ↑ S. Amari. "Dynamics of pattern formation in lateral inhibition type neural fields" Biological Cybernetics, 27:77–87, 1977.
- ↑ Coombes, Stephen (2006). "Neural fields" (PDF). Scholarpedia. 1 (6): 1373. Bibcode:2006SchpJ...1.1373C. doi: 10.4249/scholarpedia.1373 .
- ↑ G. B. Ermentrout and J. D. Cowan. "A mathematical theory of visual hallucination patterns" Biological Cybernetics, 34:137–150, 1979.
- ↑ David H. Wolpert and Bruce J. MacLennan, "A Universal Field Computer That is Purely Linear", University of Tennessee, Knoxville, Department of Computer Science Technical Report CS-93-206, September 14, 1993, 28 pp.