
In mathematics, convolution is a mathematical operation on two functions that produces a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result. The integral is evaluated for all values of shift, producing the convolution function.
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called activity. Power is a scalar quantity.
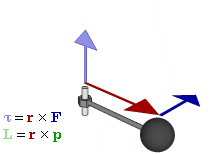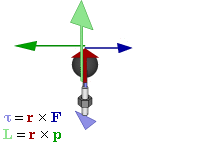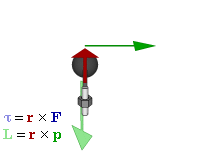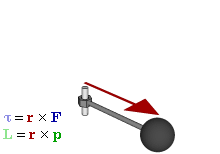
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force. It represents the capability of a force to produce change in the rotational motion of the body. The concept originated with the studies by Archimedes of the usage of levers, which is reflected in his famous quote: "Give me a lever and a place to stand and I will move the Earth". Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. Torque is defined as the product of the magnitude of the perpendicular component of the force and the distance of the line of action of a force from the point around which it is being determined. The law of conservation of energy can also be used to understand torque. The symbol for torque is typically , the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M.

In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.

In mathematics, an open set is a generalization of open interval in the real line.
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions is the pointwise product of their Fourier transforms. More generally, convolution in one domain equals point-wise multiplication in the other domain. Other versions of the convolution theorem are applicable to various Fourier-related transforms.

Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.

An instanton is a notion appearing in theoretical and mathematical physics. An instanton is a classical solution to equations of motion with a finite, non-zero action, either in quantum mechanics or in quantum field theory. More precisely, it is a solution to the equations of motion of the classical field theory on a Euclidean spacetime.

In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic.
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function (see § Definition). The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° (π⁄2 radians) to every frequency component of a function, the sign of the shift depending on the sign of the frequency (see § Relationship with the Fourier transform). The Hilbert transform is important in signal processing, where it is a component of the analytic representation of a real-valued signal u(t). The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions.

Elwyn Ralph Berlekamp was a professor of mathematics and computer science at the University of California, Berkeley. Berlekamp was widely known for his work in computer science, coding theory and combinatorial game theory.
The representation theory of groups is a part of mathematics which examines how groups act on given structures.

The Ramanujan tau function, studied by Ramanujan (1916), is the function :\mathbb {N} \rightarrow \mathbb {Z} } defined by the following identity:

In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined below. These properties apply (exactly or approximately) to many important physical systems, in which case the response y(t) of the system to an arbitrary input x(t) can be found directly using convolution: y(t) = (x ∗ h)(t) where h(t) is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication, as is frequently employed by the symbol in computer languages). What's more, there are systematic methods for solving any such system (determining h(t)), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers.

In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.
In mathematics, the Gateaux differential or Gateaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gateaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector spaces such as Banach spaces. Like the Fréchet derivative on a Banach space, the Gateaux differential is often used to formalize the functional derivative commonly used in the calculus of variations and physics.

A triangular function is a function whose graph takes the shape of a triangle. Often this is an isosceles triangle of height 1 and base 2 in which case it is referred to as the triangular function. Triangular functions are useful in signal processing and communication systems engineering as representations of idealized signals, and the triangular function specifically as an integral transform kernel function from which more realistic signals can be derived, for example in kernel density estimation. It also has applications in pulse-code modulation as a pulse shape for transmitting digital signals and as a matched filter for receiving the signals. It is also used to define the triangular window sometimes called the Bartlett window.
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; in particular, every local martingale that is bounded from below is a supermartingale, and every local martingale that is bounded from above is a submartingale; however, in general a local martingale is not a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process is a local martingale, but not necessarily a martingale.
A Modified Wigner distribution function is a variation of the Wigner distribution function (WD) with reduced or removed cross-terms.
Blockbusting is a solved combinatorial game introduced in 1987 by Elwyn Berlekamp illustrating a generalisation of overheating.



































