
Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it normally refers to the degree to which a pair of variables are linearly related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It is often used when the search space is discrete. For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms such as gradient descent or branch and bound.
In mathematical optimization and decision theory, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite, in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy.
In the field of mathematical optimization, stochastic programming is a framework for modeling optimization problems that involve uncertainty. A stochastic program is an optimization problem in which some or all problem parameters are uncertain, but follow known probability distributions. This framework contrasts with deterministic optimization, in which all problem parameters are assumed to be known exactly. The goal of stochastic programming is to find a decision which both optimizes some criteria chosen by the decision maker, and appropriately accounts for the uncertainty of the problem parameters. Because many real-world decisions involve uncertainty, stochastic programming has found applications in a broad range of areas ranging from finance to transportation to energy optimization.
In the domain of physics and probability, a Markov random field (MRF), Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. In other words, a random field is said to be a Markov random field if it satisfies Markov properties. The concept originates from the Sherrington–Kirkpatrick model.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.

In probability theory and machine learning, the multi-armed bandit problem is a problem in which a fixed limited set of resources must be allocated between competing (alternative) choices in a way that maximizes their expected gain, when each choice's properties are only partially known at the time of allocation, and may become better understood as time passes or by allocating resources to the choice. This is a classic reinforcement learning problem that exemplifies the exploration–exploitation tradeoff dilemma. The name comes from imagining a gambler at a row of slot machines, who has to decide which machines to play, how many times to play each machine and in which order to play them, and whether to continue with the current machine or try a different machine. The multi-armed bandit problem also falls into the broad category of stochastic scheduling.

In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
Stochastic control or stochastic optimal control is a sub field of control theory that deals with the existence of uncertainty either in observations or in the noise that drives the evolution of the system. The system designer assumes, in a Bayesian probability-driven fashion, that random noise with known probability distribution affects the evolution and observation of the state variables. Stochastic control aims to design the time path of the controlled variables that performs the desired control task with minimum cost, somehow defined, despite the presence of this noise. The context may be either discrete time or continuous time.
In mathematics, the Fortuin–Kasteleyn–Ginibre (FKG) inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics, due to Cees M. Fortuin, Pieter W. Kasteleyn, and Jean Ginibre (1971). Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated. It was obtained by studying the random cluster model.
The scenario approach or scenario optimization approach is a technique for obtaining solutions to robust optimization and chance-constrained optimization problems based on a sample of the constraints. It also relates to inductive reasoning in modeling and decision-making. The technique has existed for decades as a heuristic approach and has more recently been given a systematic theoretical foundation.
In mathematics, a submodular set function is a set function whose value, informally, has the property that the difference in the incremental value of the function that a single element makes when added to an input set decreases as the size of the input set increases. Submodular functions have a natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory and electrical networks. Recently, submodular functions have also found immense utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains.
Financial correlations measure the relationship between the changes of two or more financial variables over time. For example, the prices of equity stocks and fixed interest bonds often move in opposite directions: when investors sell stocks, they often use the proceeds to buy bonds and vice versa. In this case, stock and bond prices are negatively correlated.
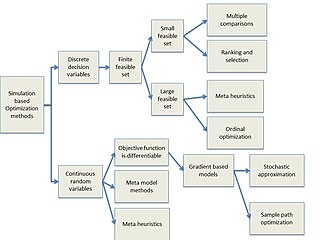
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.
Bayesian-optimal pricing is a kind of algorithmic pricing in which a seller determines the sell-prices based on probabilistic assumptions on the valuations of the buyers. It is a simple kind of a Bayesian-optimal mechanism, in which the price is determined in advance without collecting actual buyers' bids.
Stochastic scheduling concerns scheduling problems involving random attributes, such as random processing times, random due dates, random weights, and stochastic machine breakdowns. Major applications arise in manufacturing systems, computer systems, communication systems, logistics and transportation, machine learning, etc.
Probabilistic numerics is a scientific field at the intersection of statistics, machine learning and applied mathematics, where tasks in numerical analysis including finding numerical solutions for integration, linear algebra, optimisation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.










