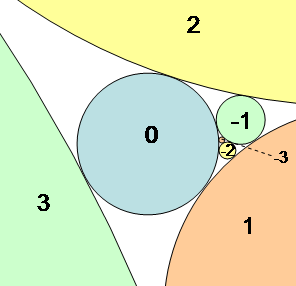
In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.





