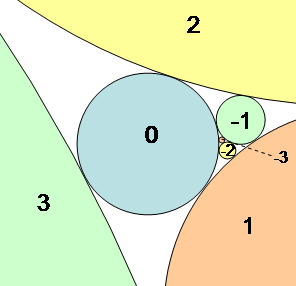
In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.
The radii of the circles in the sequence form a geometric progression with ratio
where is the golden ratio. This ratio and its reciprocal satisfy the equation
and so any four consecutive circles in the sequence meet the conditions of Descartes' theorem. [1] [2]
The centres of the circles in the sequence lie on a logarithmic spiral. Viewed from the centre of the spiral, the angle between the centres of successive circles is [1]
The angle between consecutive triples of centers is
the same as one of the angles of the Kepler triangle, a right triangle whose construction also involves the square root of the golden ratio. [3]
The construction is named after geometer H. S. M. Coxeter, who generalised the two-dimensional case to sequences of spheres and hyperspheres in higher dimensions. [1] [4] [5] It can be interpreted as a degenerate special case of the Doyle spiral. [2]
In mathematics, the Fibonacci numbers, commonly denoted Fn , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors omit the initial terms and start the sequence from 1 and 1 or from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with
The Mercator projection is a cylindrical map projection presented by Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for navigation because it is unique in representing north as up and south as down everywhere while preserving local directions and shapes. The map is thereby conformal. As a side effect, the Mercator projection inflates the size of objects away from the equator. This inflation is very small near the equator but accelerates with increasing latitude to become infinite at the poles. As a result, landmasses such as Greenland, Antarctica and Russia appear far larger than they actually are relative to landmasses near the equator, such as Central Africa.
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.
In mathematics, the tangent space of a manifold generalizes to higher dimensions the notion of tangent planes to surfaces in three dimensions and tangent lines to curves in two dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line". More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral".
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.
A hyperbolic spiral is a plane curve, which can be described in polar coordinates by the equation
A Fermat's spiral or parabolic spiral is a plane curve with the property that the area between any two consecutive full turns around the spiral is invariant. As a result, the distance between turns grows in inverse proportion to their distance from the spiral center, contrasting with the Archimedean spiral and the logarithmic spiral. Fermat spirals are named after Pierre de Fermat.
In navigation, a rhumb line, rhumb, or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north.
In geometry, the golden angle is the smaller of the two angles created by sectioning the circumference of a circle according to the golden ratio; that is, into two arcs such that the ratio of the length of the smaller arc to the length of the larger arc is the same as the ratio of the length of the larger arc to the full circumference of the circle.
In mathematics, a Ford circle is a circle with center at and radius where is an irreducible fraction, i.e. and are coprime integers. Each Ford circle is tangent to the horizontal axis and any two Ford circles are either tangent or disjoint from each other.
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
In geometry, Villarceau circles are a pair of circles produced by cutting a torus obliquely through the center at a special angle.
The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, the concept of scale becomes meaningful in two distinct ways.
In astronomy, position angle is the convention for measuring angles on the sky. The International Astronomical Union defines it as the angle measured relative to the north celestial pole (NCP), turning positive into the direction of the right ascension. In the standard (non-flipped) images, this is a counterclockwise measure relative to the axis into the direction of positive declination.
A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression is where is the golden ratio, and the progression can be written: , or approximately . Squares on the edges of this triangle have areas in another geometric progression, . Alternative definitions of the same triangle characterize it in terms of the three Pythagorean means of two numbers, or via the inradius of isosceles triangles.
In mathematics, a conical spiral, also known as a conical helix, is a space curve on a right circular cone, whose floor plan is a plane spiral. If the floor plan is a logarithmic spiral, it is called conchospiral.
In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.
