
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word partial in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.
In mathematics, a total order, simple order, linear order, connex order, or full order is a binary relation on some set , which is antisymmetric, transitive, and a connex relation. A set paired with a total order is called a chain, a totally ordered set, a simply ordered set, a linearly ordered set, or a loset.

In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set (poset) is an element of S that is not smaller than any other element in S. A minimal element of a subset S of some partially ordered set is defined dually as an element of S that is not greater than any other element in S.
Order theory is a branch of mathematics which investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field that provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum and a unique infimum. An example is given by the natural numbers, partially ordered by divisibility, for which the unique supremum is the least common multiple and the unique infimum is the greatest common divisor.
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).

In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets and are in turn generalized by partially ordered sets and preorders.
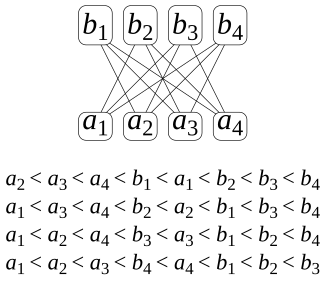
In mathematics, the dimension of a partially ordered set (poset) is the smallest number of total orders the intersection of which gives rise to the partial order. This concept is also sometimes called the order dimension or the Dushnik–Miller dimension of the partial order. Dushnik & Miller (1941) first studied order dimension; for a more detailed treatment of this subject than provided here, see Trotter (1992).

In mathematics, any two elements x and y of a set P that is partially ordered by a binary relation ≤ are comparable when either x ≤ y or y ≤ x. If it is not the case that x and y are comparable, then they are called incomparable.
In mathematics, a partial order or total order < on a set is said to be dense if, for all and in for which , there is a in such that . That is, for any two elements, one less than the other, there is another element between them. For total orders we can say this more simply as "for any two distinct elements, there is another element between them", since totality implies that two distinct elements are related by , but this is false in general for partial orders because distinct elements can be incomparable.
In mathematics, a representation is a very general relationship that expresses similarities between mathematical objects or structures. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the representing objects yi conform, in some consistent way, to those existing among the corresponding represented objects xi. More specifically, given a set Π of properties and relations, a Π-representation of some structure X is a structure Y that is the image of X under a homomorphism that preserves Π. The label representation is sometimes also applied to the homomorphism itself.
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order. Comparability graphs have also been called transitively orientable graphs, partially orderable graphs, containment graphs, and divisor graphs. An incomparability graph is an undirected graph that connects pairs of elements that are not comparable to each other in a partial order.
In mathematics, a Riesz space, lattice-ordered vector space or vector lattice is a partially ordered vector space where the order structure is a lattice.
In order theory, a branch of mathematics, a linear extension of a partial order is a total order that is compatible with the partial order. As a classic example, the lexicographic order of totally ordered sets is a linear extension of their product order.
In mathematics, the Szpilrajn extension theorem, proved by Edward Szpilrajn in 1930, states that every partial order is contained in a total order. Intuitively, the theorem says that any method of comparing elements that leaves some pairs incomparable can be extended in such a way that every pair becomes comparable. The theorem is one of many examples of the use of the axiom of choice in the form of Zorn's lemma to find a maximal set with certain properties.
In order theory, a branch of mathematics, the 1/3–2/3 conjecture states that, if one is comparison sorting a set of items then, no matter what comparisons may have already been performed, it is always possible to choose the next comparison in such a way that it will reduce the number of possible sorted orders by a factor of 2/3 or better. Equivalently, in every finite partially ordered set that is not totally ordered, there exists a pair of elements x and y with the property that at least 1/3 and at most 2/3 of the linear extensions of the partial order place x earlier than y.
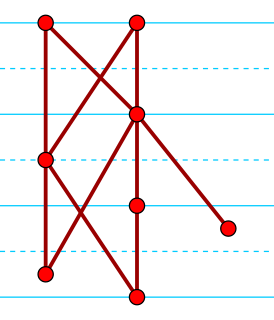
In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce (1956) as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.

In order-theoretic mathematics, a series-parallel partial order is a partially ordered set built up from smaller series-parallel partial orders by two simple composition operations.
In mathematics, the order polytope of a finite partially ordered set is a convex polytope defined from the set. The points of the order polytope are the monotonic functions from the given set to the unit interval, its vertices correspond to the upper sets of the partial order, and its dimension is the number of elements in the partial order. The order polytope is a distributive polytope, meaning that coordinatewise minima and maxima of pairs of its points remain within the polytope.







