Cumulative prospect theory

Last updated June 02, 2022

Cumulative prospect theory (CPT) is a model for descriptive decisions under risk and uncertainty which was introduced by Amos Tversky and Daniel Kahneman in 1992 (Tversky, Kahneman, 1992). It is a further development and variant of prospect theory. The difference between this version and the original version of prospect theory is that weighting is applied to the cumulative probability distribution function, as in rank-dependent expected utility theory but not applied to the probabilities of individual outcomes. In 2002, Daniel Kahneman received the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel for his contributions to behavioral economics, in particular the development of Cumulative Prospect Theory (CPT).

Outline of the model

The main observation of CPT (and its predecessor prospect theory) is that people tend to think of possible outcomes usually relative to a certain reference point (often the status quo) rather than to the final status, a phenomenon which is called framing effect. Moreover, they have different risk attitudes towards gains (i.e. outcomes above the reference point) and losses (i.e. outcomes below the reference point) and care generally more about potential losses than potential gains (loss aversion). Finally, people tend to overweight extreme events, but underweight "average" events. The last point is in contrast to Prospect Theory which assumes that people overweight unlikely events, independently of their relative outcomes.

CPT incorporates these observations in a modification of expected utility theory by replacing final wealth with payoffs relative to the reference point, replacing the utility function with a value function that depends on relative payoff, and replacing cumulative probabilities with weighted cumulative probabilities. In the general case, this leads to the following formula for subjective utility of a risky outcome described by probability measure $p$ :

$U(p):=\int _{-\infty }^{0}v(x){\frac {d}{dx}}(w(F(x)))\,dx+\int _{0}^{+\infty }v(x){\frac {d}{dx}}(-w(1-F(x)))\,dx,$

where $v$ is the value function (typical form shown in Figure 1), $w$ is the weighting function (as sketched in Figure 2) and $F(x):=\int _{-\infty }^{x}\,dp$ , i.e. the integral of the probability measure over all values up to $x$ , is the cumulative probability. This generalizes the original formulation by Tversky and Kahneman from finitely many distinct outcomes to infinite (i.e., continuous) outcomes.

Differences from prospect theory

The main modification to prospect theory is that, as in rank-dependent expected utility theory, cumulative probabilities are transformed, rather than the probabilities themselves. This leads to the aforementioned overweighting of extreme events which occur with small probability, rather than to an overweighting of all small probability events. The modification helps to avoid a violation of first order stochastic dominance and makes the generalization to arbitrary outcome distributions easier. CPT is, therefore, an improvement over Prospect Theory on theoretical grounds.

Applications

Cumulative prospect theory has been applied to a diverse range of situations which appear inconsistent with standard economic rationality, in particular the equity premium puzzle, the asset allocation puzzle, the status quo bias, various gambling and betting puzzles, intertemporal consumption and the endowment effect.

Parameters for cumulative prospect theory have been estimated for a large number of countries,^[1] demonstrating the broad validity of the theory.

Related Research Articles

In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable $, or just distribution function of, evaluated at, is the probability that will take a value less than or equal to .$

In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable.

In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable $, which takes values in the alphabet and is distributed according to :$

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

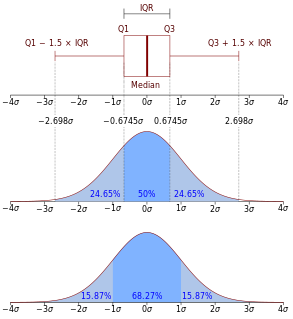
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be close to that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.

In both economics and finance, "risk aversion" is the tendency of people and those economic agents to choose outcomes with low uncertainty over high uncertainty, even if the monetary value of the uncertainty average outcome is equal to or even higher than the value of the more certain outcome. Formally, risk averse people have a stronger preference for expected value. The expected value of risk is used to predict the uncertainty of the risk loss or gain of the gamble itself, and is equal to the potential payoff multiplied by the sum of each probability. Risk aversion comprehensively explains people's tendency in agreeing to a more predictable but potentially with a lower payoff situation, rather than agreeing to a highly unpredictable but potentially a higher payoff situation. For example, investors who are risk-averse may prefer to deposit their funds in a potentially lower interest rate but more assured bank account, rather than depositing into a stock account, but may involve the opportunity in losing value (risky). Risk aversion is the concept that people prefer to gamble with certainty and plus with the same expected value.

Prospect theory is a theory of behavioral economics and behavioral finance that was developed by Daniel Kahneman and Amos Tversky in 1979. The theory was cited in the decision to award Kahneman the 2002 Nobel Memorial Prize in Economics.

The St. Petersburg paradox or St. Petersburg lottery is a paradox involving the game of flipping a coin where the expected payoff of the theoretical lottery game approaches infinity but nevertheless seems to be worth only a very small amount to the participants. The St. Petersburg paradox is a situation where a naive decision criterion which takes only the expected value into account predicts a course of action that presumably no actual person would be willing to take. It is related to probability and decision theory in economics. Several resolutions to the paradox have been proposed.

The expected utility hypothesis is a popular concept in economics that serves as a reference guide for decisions when the payoff is uncertain. The theory recommends which option rational individuals should choose in a complex situation, based on their risk appetite and preferences.

In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions. The larger the scale parameter, the more spread out the distribution.

In quantum mechanics, information theory, and Fourier analysis, the entropic uncertainty or Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle can be expressed as a lower bound on the sum of these entropies. This is stronger than the usual statement of the uncertainty principle in terms of the product of standard deviations.

The Allais paradox is a choice problem designed by Maurice Allais (1953) to show an inconsistency of actual observed choices with the predictions of expected utility theory.

Differential entropy is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy.

Stochastic dominance is a partial order between random variables. It is a form of stochastic ordering. The concept arises in decision theory and decision analysis in situations where one gamble can be ranked as superior to another gamble for a broad class of decision-makers. It is based on shared preferences regarding sets of possible outcomes and their associated probabilities. Only limited knowledge of preferences is required for determining dominance. Risk aversion is a factor only in second order stochastic dominance.

The rank-dependent expected utility model is a generalized expected utility model of choice under uncertainty, designed to explain the behaviour observed in the Allais paradox, as well as for the observation that many people both purchase lottery tickets and insure against losses.

A Choquet integral is a subadditive or superadditive integral created by the French mathematician Gustave Choquet in 1953. It was initially used in statistical mechanics and potential theory, but found its way into decision theory in the 1980s, where it is used as a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions and capacities. In imprecise probability theory, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone lower probability, or the upper expectation induced by a 2-alternating upper probability.

In quantum mechanics, the expectation value is the probabilistic expected value of the result (measurement) of an experiment. It can be thought of as an average of all the possible outcomes of a measurement as weighted by their likelihood, and as such it is not the most probable value of a measurement; indeed the expectation value may have zero probability of occurring. It is a fundamental concept in all areas of quantum physics.

In decision theory, the expected value of sample information (EVSI) is the expected increase in utility that a decision-maker could obtain from gaining access to a sample of additional observations before making a decision. The additional information obtained from the sample may allow them to make a more informed, and thus better, decision, thus resulting in an increase in expected utility. EVSI attempts to estimate what this improvement would be before seeing actual sample data; hence, EVSI is a form of what is known as preposterior analysis.

In probability theory and statistics, the law of the unconscious statistician, or LOTUS, is a theorem used to calculate the expected value of a function g(X) of a random variable X when one knows the probability distribution of X but one does not know the distribution of g(X). The form of the law can depend on the form in which one states the probability distribution of the random variable X. If it is a discrete distribution and one knows its probability mass function ƒ_X, then the expected value of g(X) is

Risk aversion is a preference for a sure outcome over a gamble with higher or equal expected value. Conversely, the rejection of a sure thing in favor of a gamble of lower or equal expected value is known as risk-seeking behavior.

References

↑ Rieger, M., Wang, M. & Hens, T. (2017). Estimating Cumulative Prospect Theory Parameters from an International Survey. Theory and Decision, 82, 4, 567-596.

Tversky, Amos; Kahneman, Daniel (1992). "Advances in prospect theory: Cumulative representation of uncertainty". Journal of Risk and Uncertainty. 5 (4): 297–323. doi:10.1007/BF00122574. S2CID 8456150.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Rieger, M., Wang, M. & Hens, T. (2017). Estimating Cumulative Prospect Theory Parameters from an International Survey. Theory and Decision, 82, 4, 567-596.

[1]