
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, for independent and identically distributed random variables, the sampling distribution of the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.

A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs now." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov.
In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.
In linear algebra, an n-by-n square matrix A is called invertible, if there exists an n-by-n square matrix B such that
In mathematics, and in particular linear algebra, the Moore–Penrose inverse of a matrix is the most widely known generalization of the inverse matrix. It was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951, and Roger Penrose in 1955. Earlier, Erik Ivar Fredholm had introduced the concept of a pseudoinverse of integral operators in 1903. When referring to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose inverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse.
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by ρ(·).
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).
In mathematical analysis, Cesàro summation assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as n tends to infinity, of the sequence of arithmetic means of the first n partial sums of the series.
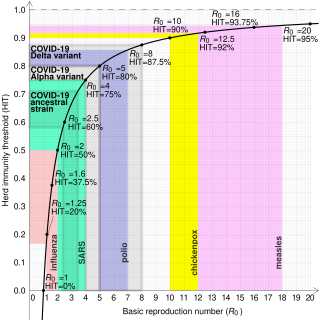
In epidemiology, the basic reproduction number, or basic reproductive number, denoted , of an infection is the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection. The definition assumes that no other individuals are infected or immunized. Some definitions, such as that of the Australian Department of Health, add the absence of "any deliberate intervention in disease transmission". The basic reproduction number is not necessarily the same as the effective reproduction number , which is the number of cases generated in the current state of a population, which does not have to be the uninfected state. is a dimensionless number and not a time rate, which would have units of time−1, or units of time like doubling time.
A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state.
In matrix theory, the Perron–Frobenius theorem, proved by Oskar Perron (1907) and Georg Frobenius (1912), asserts that a real square matrix with positive entries has a unique eigenvalue of largest magnitude and that eigenvalue is real. The corresponding eigenvector can be chosen to have strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory ; to the theory of dynamical systems ; to economics ; to demography ; to social networks ; to Internet search engines (PageRank); and even to ranking of football teams. The first to discuss the ordering of players within tournaments using Perron–Frobenius eigenvectors is Edmund Landau.
In mathematics, the Silverman–Toeplitz theorem, first proved by Otto Toeplitz, is a result in summability theory characterizing matrix summability methods that are regular. A regular matrix summability method is a matrix transformation of a convergent sequence which preserves the limit.
A Neumann series is a mathematical series of the form
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product BB is equal to A.
In mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and those matrices that do have a logarithm may have more than one logarithm. The study of logarithms of matrices leads to Lie theory since when a matrix has a logarithm then it is in an element of a Lie group and the logarithm is the corresponding element of the vector space of the Lie algebra.

In probability, a discrete-time Markov chain (DTMC) is a sequence of random variables, known as a stochastic process, in which the value of the next variable depends only on the value of the current variable, and not any variables in the past. For instance, a machine may have two states, A and E. When it is in state A, there is a 40% chance of it moving to state E and a 60% chance of it remaining in state A. When it is in state E, there is a 70% chance of it moving to A and a 30% chance of it staying in E. The sequence of states of the machine is a Markov chain. If we denote the chain by then is the state which the machine starts in and is the random variable describing its state after 10 transitions. The process continues forever, indexed by the natural numbers.
In numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix. It is named after Carl Gustav Jacob Jacobi, who first proposed the method in 1846, but only became widely used in the 1950s with the advent of computers.
In the mathematical theory of probability, the entropy rate or source information rate of a stochastic process is, informally, the time density of the average information in a stochastic process. For stochastic processes with a countable index, the entropy rate is the limit of the joint entropy of members of the process divided by , as tends to infinity:
In linear algebra, a convergent matrix is a matrix that converges to the zero matrix under matrix exponentiation.



















































