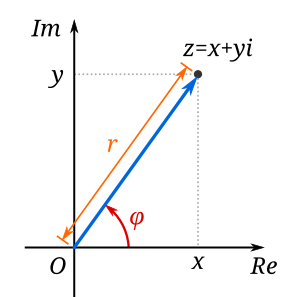
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution, Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution is the distribution of the x-intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables if the denominator distribution has mean zero.
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.

In complex analysis, a discipline within mathematics, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. From a geometrical perspective, it is a special case of the generalized Stokes' theorem.
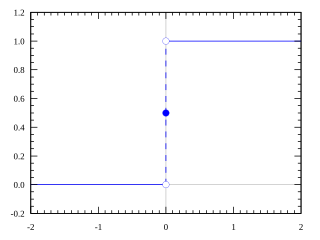
The Heaviside step function, or the unit step function, usually denoted by H or θ, is a discontinuous function, named after Oliver Heaviside (1850–1925), whose value is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one.

In mathematics, the error function is a special function (non-elementary) of sigmoid shape that occurs in probability, statistics, and partial differential equations describing diffusion. It is defined as:
Integration is the basic operation in integral calculus. While differentiation has easy rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.
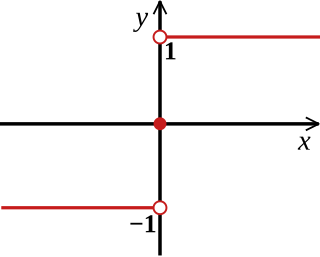
In mathematics, the sign function or signum function is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as sgn.
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function :

In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
In mathematics, the binomial series is the Maclaurin series for the function given by , where is an arbitrary complex number. Explicitly,
In control theory, a state observer is a system that provides an estimate of the internal state of a given real system, from measurements of the input and output of the real system. It is typically computer-implemented, and provides the basis of many practical applications.
Linear time-invariant theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant system to an arbitrary input signal. Trajectories of these systems are commonly measured and tracked as they move through time, but in applications like image processing and field theory, the LTI systems also have trajectories in spatial dimensions. Thus, these systems are also called linear translation-invariant to give the theory the most general reach. In the case of generic discrete-time systems, linear shift-invariant is the corresponding term. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors.
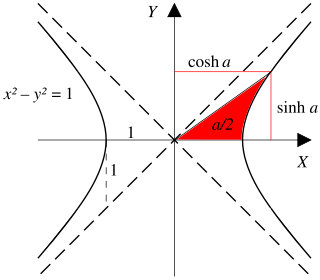
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions.

In mathematics, the concept of sign originates from the property of every real number being either positive or negative or zero. Depending on local conventions, zero is either considered as being neither a positive, nor a negative number, or as belonging to both, negative and positive numbers. If not specifically mentioned this article adheres to the first convention. In some contexts it makes sense to consider a signed zero, e.g., in floating point representations of real numbers within computers. The phrase "change of sign" is associated throughout mathematics and physics to generate the additive inverse of any object that allows for this construction, and is not restricted to real numbers. It applies among other objects to vectors, matrices, and complex numbers, which are not prescribed to be only either positive, negative, or zero. The word "sign" is also often used to indicate other binary aspects of mathematical objects that resemble positivity and negativity, such as odd and even, sense of orientation or rotation (cw/ccw), one sided limits, and others, below.
In mathematics, undefined has several different meanings, depending on the context. Such contexts include the following, among others:
In probability theory and directional statistics, a wrapped Lévy distribution is a wrapped probability distribution that results from the "wrapping" of the Lévy distribution around the unit circle.