
Molecular diffusion, often simply called diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a phase with uniform temperature, absent external net forces acting on the particles, the diffusion process will eventually result in complete mixing.

Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.
In continuum mechanics, the Péclet number is a class of dimensionless numbers relevant in the study of transport phenomena in a continuum. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient. In the context of species or mass transfer, the Péclet number is the product of the Reynolds number and the Schmidt number. In the context of the thermal fluids, the thermal Péclet number is equivalent to the product of the Reynolds number and the Prandtl number.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its thermal conductivity, and is denoted k.

In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
There are two different Bejan numbers (Be) used in the scientific domains of thermodynamics and fluid mechanics. Bejan numbers are named after Adrian Bejan.

The plug flow reactor model is a model used to describe chemical reactions in continuous, flowing systems of cylindrical geometry. The PFR model is used to predict the behavior of chemical reactors of such design, so that key reactor variables, such as the dimensions of the reactor, can be estimated.

In hydrodynamics, a plume or a column is a vertical body of one fluid moving through another. Several effects control the motion of the fluid, including momentum (inertia), diffusion and buoyancy. Pure jets and pure plumes define flows that are driven entirely by momentum and buoyancy effects, respectively. Flows between these two limits are usually described as forced plumes or buoyant jets. "Buoyancy is defined as being positive" when, in the absence of other forces or initial motion, the entering fluid would tend to rise. Situations where the density of the plume fluid is greater than its surroundings, but the flow has sufficient initial momentum to carry it some distance vertically, are described as being negatively buoyant.
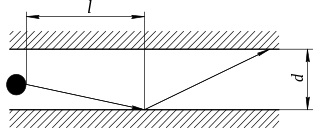
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore with a narrow diameter (2–50 nm) because molecules frequently collide with the pore wall. As another example, consider the diffusion of gas molecules through very small capillary pores. If the pore diameter is smaller than the mean free path of the diffusing gas molecules, and the density of the gas is low, the gas molecules collide with the pore walls more frequently than with each other, leading to Knudsen diffusion.

In fluid dynamics, eddy diffusion, eddy dispersion, or turbulent diffusion is a process by which fluid substances mix together due to eddy motion. These eddies can vary widely in size, from subtropical ocean gyres down to the small Kolmogorov microscales, and occur as a result of turbulence. The theory of eddy diffusion was first developed by Sir Geoffrey Ingram Taylor.
Taylor dispersion or Taylor diffusion is an apparent or effective diffusion of some scalar field arising on the large scale due to the presence of a strong, confined, zero-mean shear flow on the small scale. Essentially, the shear acts to smear out the concentration distribution in the direction of the flow, enhancing the rate at which it spreads in that direction. The effect is named after the British fluid dynamicist G. I. Taylor, who described the shear-induced dispersion for large Peclet numbers. The analysis was later generalized by Rutherford Aris for arbitrary values of the Peclet number. The dispersion process is sometimes also referred to as the Taylor-Aris dispersion.

Diffusiophoresis is the spontaneous motion of colloidal particles or molecules in a fluid, induced by a concentration gradient of a different substance. In other words, it is motion of one species, A, in response to a concentration gradient in another species, B. Typically, A is colloidal particles which are in aqueous solution in which B is a dissolved salt such as sodium chloride, and so the particles of A are much larger than the ions of B. But both A and B could be polymer molecules, and B could be a small molecule. For example, concentration gradients in ethanol solutions in water move 1 μm diameter colloidal particles with diffusiophoretic velocities of order 0.1 to 1 μm/s, the movement is towards regions of the solution with lower ethanol concentration. Both species A and B will typically be diffusing but diffusiophoresis is distinct from simple diffusion: in simple diffusion a species A moves down a gradient in its own concentration.
The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
Turbulent diffusion is the transport of mass, heat, or momentum within a system due to random and chaotic time dependent motions. It occurs when turbulent fluid systems reach critical conditions in response to shear flow, which results from a combination of steep concentration gradients, density gradients, and high velocities. It occurs much more rapidly than molecular diffusion and is therefore extremely important for problems concerning mixing and transport in systems dealing with combustion, contaminants, dissolved oxygen, and solutions in industry. In these fields, turbulent diffusion acts as an excellent process for quickly reducing the concentrations of a species in a fluid or environment, in cases where this is needed for rapid mixing during processing, or rapid pollutant or contaminant reduction for safety.

Double diffusive convection is a fluid dynamics phenomenon that describes a form of convection driven by two different density gradients, which have different rates of diffusion.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.

A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor, fluidized bed reactor, and bubble column reactor. A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.
Particle-laden flows refers to a class of two-phase fluid flow, in which one of the phases is continuously connected and the other phase is made up of small, immiscible, and typically dilute particles. Fine aerosol particles in air is an example of a particle-laden flow; the aerosols are the dispersed phase, and the air is the carrier phase.











