Acoustic theory is a scientific field that relates to the description of sound waves. It derives from fluid dynamics. See acoustics for the engineering approach.
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of viscous fluid substances.

In fluid dynamics, the Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. The equations represent Cauchy equations of conservation of mass (continuity), and balance of momentum and energy, and can be seen as particular Navier–Stokes equations with zero viscosity and zero thermal conductivity. In fact, Euler equations can be obtained by linearization of some more precise continuity equations like Navier–Stokes equations in a local equilibrium state given by a Maxwellian. The Euler equations can be applied to incompressible and to compressible flow – assuming the flow velocity is a solenoidal field, or using another appropriate energy equation respectively. Historically, only the incompressible equations have been derived by Euler. However, fluid dynamics literature often refers to the full set – including the energy equation – of the more general compressible equations together as "the Euler equations".
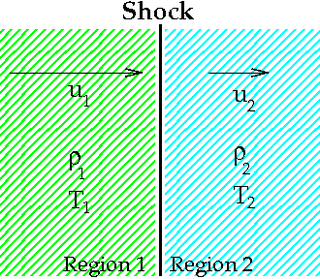
The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a shock wave or a combustion wave in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine and French engineer Pierre Henri Hugoniot.
The geostrophic wind is the theoretical wind that would result from an exact balance between the Coriolis force and the pressure gradient force. This condition is called geostrophic balance. The geostrophic wind is directed parallel to isobars. This balance seldom holds exactly in nature. The true wind almost always differs from the geostrophic wind due to other forces such as friction from the ground. Thus, the actual wind would equal the geostrophic wind only if there were no friction and the isobars were perfectly straight. Despite this, much of the atmosphere outside the tropics is close to geostrophic flow much of the time and it is a valuable first approximation. Geostrophic flow in air or water is a zero-frequency inertial wave.
Darcy's law is an equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences.

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.
Used in hydrogeology, the groundwater flow equation is the mathematical relationship which is used to describe the flow of groundwater through an aquifer. The transient flow of groundwater is described by a form of the diffusion equation, similar to that used in heat transfer to describe the flow of heat in a solid. The steady-state flow of groundwater is described by a form of the Laplace equation, which is a form of potential flow and has analogs in numerous fields.

The Chapman–Jouguet condition holds approximately in detonation waves in high explosives. It states that the detonation propagates at a velocity at which the reacting gases just reach sonic velocity as the reaction ceases.

Ekman transport, part of Ekman motion theory first investigated in 1902 by Vagn Walfrid Ekman, refers to the wind-driven net transport of the surface layer of a fluid that, due to the Coriolis effect, occurs at 90° to the direction of the surface wind. This phenomenon was first noted by Fridtjof Nansen, who recorded that ice transport appeared to occur at an angle to the wind direction during his Arctic expedition during the 1890s. The direction of transport is dependent on the hemisphere: in the northern hemisphere, transport occurs at 90° clockwise from wind direction, while in the southern hemisphere it occurs at a 90° counterclockwise.

The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum. In convective form it is written:

The theory of special relativity plays an important role in the modern theory of classical electromagnetism. First of all, it gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of reference to another. Secondly, it sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electrostatic or magnetic laws. Third, it motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.
The power law scheme was first used by Suhas Patankar (1980). It helps in achieving approximate solutions in computational fluid dynamics (CFD) and it is used for giving a more accurate approximation to the one-dimensional exact solution when compared to other schemes in computational fluid dynamics (CFD). This scheme is based on the analytical solution of the convection diffusion equation. This scheme is also very effective in removing False diffusion error.
Von Kármán swirling flow is a flow created by a uniformly rotating infinitely long plane disk, named after Theodore von Kármán who solved the problem in 1921. This problem is used as a model for centrifugal fans or compressors. This flow is classified under the category of steady flows in which vorticity generated at a solid surface is prevented from diffusing far away by an opposing convection, the other examples being the Blasius boundary layer with suction, stagnation point flow etc.


















