Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
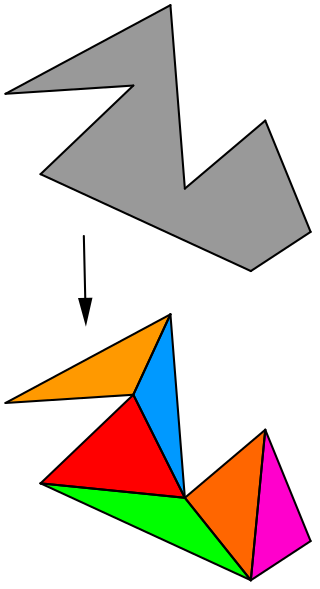
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
In computational complexity theory, L is the complexity class containing decision problems that can be solved by a deterministic Turing machine using a logarithmic amount of writable memory space. Formally, the Turing machine has two tapes, one of which encodes the input and can only be read, whereas the other tape has logarithmic size but can be read as well as written. Logarithmic space is sufficient to hold a constant number of pointers into the input and a logarithmic number of boolean flags, and many basic logspace algorithms use the memory in this way.

In geometry, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction as C at these points. That is, L is a tangent line at P and at Q.

In computational geometry, Klee's measure problem is the problem of determining how efficiently the measure of a union of (multidimensional) rectangular ranges can be computed. Here, a d-dimensional rectangular range is defined to be a Cartesian product of d intervals of real numbers, which is a subset of Rd.

In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.

In computer science, the range searching problem consists of processing a set S of objects, in order to determine which objects from S intersect with a query object, called the range. For example, if S is a set of points corresponding to the coordinates of several cities, find the subset of cities within a given range of latitudes and longitudes.
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.
In computer science, an output-sensitive algorithm is an algorithm whose running time depends on the size of the output, instead of, or in addition to, the size of the input. For certain problems where the output size varies widely, for example from linear in the size of the input to quadratic in the size of the input, analyses that take the output size explicitly into account can produce better runtime bounds that differentiate algorithms that would otherwise have identical asymptotic complexity.

Kenneth Lee Clarkson is an American computer scientist known for his research in computational geometry. He is a researcher at the IBM Almaden Research Center, and co-editor-in-chief of Discrete and Computational Geometry and of the Journal of Computational Geometry.
In computer science, the all nearest smaller values problem is the following task: for each position in a sequence of numbers, search among the previous positions for the last position that contains a smaller value. This problem can be solved efficiently both by parallel and non-parallel algorithms: Berkman, Schieber & Vishkin (1993), who first identified the procedure as a useful subroutine for other parallel programs, developed efficient algorithms to solve it in the Parallel Random Access Machine model; it may also be solved in linear time on a non-parallel computer using a stack-based algorithm. Later researchers have studied algorithms to solve it in other models of parallel computation.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
In the study of algorithms, an LP-type problem is an optimization problem that shares certain properties with low-dimensional linear programs and that may be solved by similar algorithms. LP-type problems include many important optimization problems that are not themselves linear programs, such as the problem of finding the smallest circle containing a given set of planar points. They may be solved by a combination of randomized algorithms in an amount of time that is linear in the number of elements defining the problem, and subexponential in the dimension of the problem.
John E. Hershberger is an American computer scientist and software professional, a principal engineer at Mentor Graphics Corporation since 1993. He is known for his research in computational geometry and algorithm engineering.
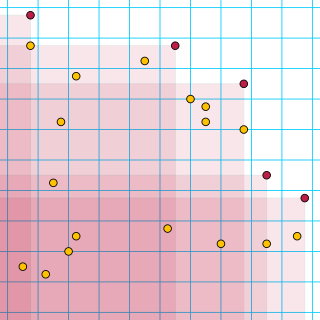
In computational geometry, a point p in a finite set of points S is said to be maximal or non-dominated if there is no other point q in S whose coordinates are all greater than or equal to the corresponding coordinates of p. The maxima of a point setS are all the maximal points of S. The problem of finding all maximal points, sometimes called the problem of the maxima or maxima set problem, has been studied as a variant of the convex hull and orthogonal convex hull problems. It is equivalent to finding the Pareto frontier of a collection of points, and was called the floating-currency problem by Herbert Freeman based on an application involving comparing the relative wealth of individuals with different holdings of multiple currencies.
In the design and analysis of algorithms for combinatorial optimization, parametric search is a technique invented by Nimrod Megiddo for transforming a decision algorithm into an optimization algorithm. It is frequently used for solving optimization problems in computational geometry.

In discrete geometry and computational geometry, the relative convex hull or geodesic convex hull is an analogue of the convex hull for the points inside a simple polygon or a rectifiable simple closed curve.
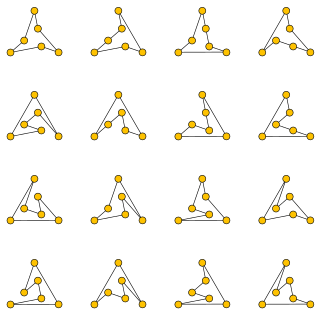
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.












