Sorting refers to ordering data in an increasing or decreasing manner according to some linear relationship among the data items.
Ordering items is the combination of categorizing them based on equivalent order, and ordering the categories themselves.
In computer science , arranging in an ordered sequence is called "sorting". Sorting is a common operation in many applications, and efficient algorithms have been developed to perform it.
The most common uses of sorted sequences are:
The opposite of sorting, rearranging a sequence of items in a random or meaningless order, is called shuffling.
For sorting, either a weak order, "should not come after", can be specified, or a strict weak order, "should come before" (specifying one defines also the other, the two are the complement of the inverse of each other, see operations on binary relations). For the sorting to be unique, these two are restricted to a total order and a strict total order, respectively.
Sorting n-tuples (depending on context also called e.g. records consisting of fields) can be done based on one or more of its components. More generally objects can be sorted based on a property. Such a component or property is called a sort key.
For example, the items are books, the sort key is the title, subject or author, and the order is alphabetical.
A new sort key can be created from two or more sort keys by lexicographical order. The first is then called the primary sort key, the second the secondary sort key, etc.
For example, addresses could be sorted using the city as primary sort key, and the street as secondary sort key.
If the sort key values are totally ordered, the sort key defines a weak order of the items: items with the same sort key are equivalent with respect to sorting. See also stable sorting. If different items have different sort key values then this defines a unique order of the items.
A standard order is often called ascending (corresponding to the fact that the standard order of numbers is ascending, i.e. A to Z, 0 to 9), the reverse order descending (Z to A, 9 to 0). For dates and times, ascending means that earlier values precede later ones e.g. 1/1/2000 will sort ahead of 1/1/2001.
Various sorting tasks are essential in industrial processes, such as mineral processing. For example, during the extraction of gold from ore, a device called a shaker table uses gravity, vibration, and flow to separate gold from lighter materials in the ore (sorting by size and weight). Sorting is also a naturally occurring process that results in the concentration of ore or sediment. Sorting results from the application of some criterion or differential stressors to a mass to separate it into its components based on some variable quality. Materials that are different, but only slightly so, such as the isotopes of uranium, are very difficult to separate.
Optical sorting is an automated process of sorting solid products using cameras and/or lasers and has widespread use in the food industry.[ citation needed ] Sensor-based sorting is used in mineral processing. [1]
Collation is the assembly of written information into a standard order. Many systems of collation are based on numerical order or alphabetical order, or extensions and combinations thereof. Collation is a fundamental element of most office filing systems, library catalogs, and reference books.
In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
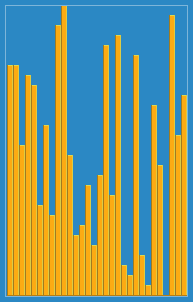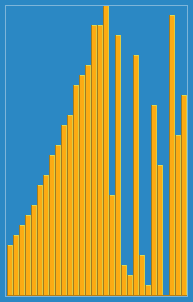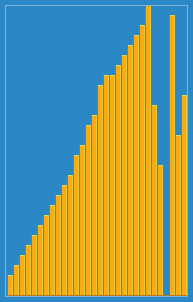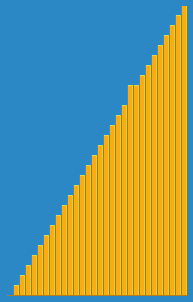
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:
In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the relative order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
In computer science, radix sort is a non-comparative sorting algorithm. It avoids comparison by creating and distributing elements into buckets according to their radix. For elements with more than one significant digit, this bucketing process is repeated for each digit, while preserving the ordering of the prior step, until all digits have been considered. For this reason, radix sort has also been called bucket sort and digital sort.
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.
In computer science, selection sort is an in-place comparison sorting algorithm. It has an O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small positive integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that possess distinct key values, and applying prefix sum on those counts to determine the positions of each key value in the output sequence. Its running time is linear in the number of items and the difference between the maximum key value and the minimum key value, so it is only suitable for direct use in situations where the variation in keys is not significantly greater than the number of items. It is often used as a subroutine in radix sort, another sorting algorithm, which can handle larger keys more efficiently.
In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".
Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
sort is a generic function in the C++ Standard Library for doing comparison sorting. The function originated in the Standard Template Library (STL).
In computing, an odd–even sort or odd–even transposition sort is a relatively simple sorting algorithm, developed originally for use on parallel processors with local interconnections. It is a comparison sort related to bubble sort, with which it shares many characteristics. It functions by comparing all odd/even indexed pairs of adjacent elements in the list and, if a pair is in the wrong order the elements are switched. The next step repeats this for even/odd indexed pairs. Then it alternates between odd/even and even/odd steps until the list is sorted.
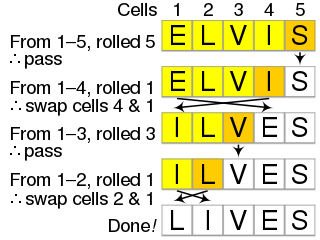
The Fisher–Yates shuffle is an algorithm for shuffling a finite sequence. The algorithm takes a list of all the elements of the sequence, and continually determines the next element in the shuffled sequence by randomly drawing an element from the list until no elements remain. The algorithm produces an unbiased permutation: every permutation is equally likely. The modern version of the algorithm takes time proportional to the number of items being shuffled and shuffles them in place.
In computer science, the all nearest smaller values problem is the following task: for each position in a sequence of numbers, search among the previous positions for the last position that contains a smaller value. This problem can be solved efficiently both by parallel and non-parallel algorithms: Berkman, Schieber & Vishkin (1993), who first identified the procedure as a useful subroutine for other parallel programs, developed efficient algorithms to solve it in the Parallel Random Access Machine model; it may also be solved in linear time on a non-parallel computer using a stack-based algorithm. Later researchers have studied algorithms to solve it in other models of parallel computation.
Timsort is a hybrid, stable sorting algorithm, derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It was implemented by Tim Peters in 2002 for use in the Python programming language. The algorithm finds subsequences of the data that are already ordered (runs) and uses them to sort the remainder more efficiently. This is done by merging runs until certain criteria are fulfilled. Timsort was Python's standard sorting algorithm from version 2.3 to version 3.10, and is used to sort arrays of non-primitive type in Java SE 7, on the Android platform, in GNU Octave, on V8, Swift, and inspired the sorting algorithm used in Rust.
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the input list element by element, comparing the current element with the one after it, swapping their values if needed. These passes through the list are repeated until no swaps have to be performed during a pass, meaning that the list has become fully sorted. The algorithm, which is a comparison sort, is named for the way the larger elements "bubble" up to the top of the list.
In computer science, partial sorting is a relaxed variant of the sorting problem. Total sorting is the problem of returning a list of items such that its elements all appear in order, while partial sorting is returning a list of the k smallest elements in order. The other elements may also be sorted, as in an in-place partial sort, or may be discarded, which is common in streaming partial sorts. A common practical example of partial sorting is computing the "Top 100" of some list.
In computer science, input enhancement is the principle that processing a given input to a problem and altering it in a specific way will increase runtime efficiency or space efficiency, or both. The altered input is usually stored and accessed to simplify the problem. By exploiting the structure and properties of the inputs, input enhancement creates various speed-ups in the efficiency of the algorithm.
In computer science, k-way merge algorithms or multiway merges are a specific type of sequence merge algorithms that specialize in taking in k sorted lists and merging them into a single sorted list. These merge algorithms generally refer to merge algorithms that take in a number of sorted lists greater than two. Two-way merges are also referred to as binary merges.The k- way merge is also an external sorting algorithm.
