A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in applied mathematics and in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right.
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of sample data. A statistical model represents, often in considerably idealized form, the data-generating process.
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles.
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution.

Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determined by comparing their results to the real-world outcomes they aim to predict. Computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics, astrophysics, climatology, chemistry, biology and manufacturing, as well as human systems in economics, psychology, social science, health care and engineering. Simulation of a system is represented as the running of the system's model. It can be used to explore and gain new insights into new technology and to estimate the performance of systems too complex for analytical solutions.
In the field of mathematical optimization, stochastic programming is a framework for modeling optimization problems that involve uncertainty. A stochastic program is an optimization problem in which some or all problem parameters are uncertain, but follow known probability distributions. This framework contrasts with deterministic optimization, in which all problem parameters are assumed to be known exactly. The goal of stochastic programming is to find a decision which both optimizes some criteria chosen by the decision maker, and appropriately accounts for the uncertainty of the problem parameters. Because many real-world decisions involve uncertainty, stochastic programming has found applications in a broad range of areas ranging from finance to transportation to energy optimization.

Minimum viable population (MVP) is a lower bound on the population of a species, such that it can survive in the wild. This term is commonly used in the fields of biology, ecology, and conservation biology. MVP refers to the smallest possible size at which a biological population can exist without facing extinction from natural disasters or demographic, environmental, or genetic stochasticity. The term "population" is defined as a group of interbreeding individuals in similar geographic area that undergo negligible gene flow with other groups of the species. Typically, MVP is used to refer to a wild population, but can also be used for ex-situ conservation.
Network traffic simulation is a process used in telecommunications engineering to measure the efficiency of a communications network.
Microsimulation is a category of computerized analytical tools that perform highly detailed analysis of activities such as highway traffic flowing through an intersection, financial transactions, or pathogens spreading disease through a population. Microsimulation is often used to evaluate the effects of proposed interventions before they are implemented in the real world. For example, a traffic microsimulation model could be used to evaluate the effectiveness of lengthening a turn lane at an intersection, and thus help decide whether it is worth spending money on actually lengthening the lane.
"Stochastic" means being or having a random variable. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. The random variation is usually based on fluctuations observed in historical data for a selected period using standard time-series techniques. Distributions of potential outcomes are derived from a large number of simulations which reflect the random variation in the input(s).
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
A tax-benefit model is a form of microsimulation model. It is usually based on a representative or administrative data set and certain policy rules. These models are used to cost certain policy reforms and to determine the winners and losers of reform. One example is EUROMOD, which models taxes and benefits for 27 EU states, and its post-Brexit offshoot, UKMOD.
In geophysics, seismic inversion is the process of transforming seismic reflection data into a quantitative rock-property description of a reservoir. Seismic inversion may be pre- or post-stack, deterministic, random or geostatistical; it typically includes other reservoir measurements such as well logs and cores.
Mobility models characterize the movements of mobile users with respect to their location, velocity and direction over a period of time. These models play an vital role in the design of Mobile Ad Hoc Networks(MANET). Most of the times simulators play a significant role in testing the features of mobile ad hoc networks. Simulators like allow the users to choose the mobility models as these models represent the movements of nodes or users. As the mobile nodes move in different directions, it becomes imperative to characterize their movements vis-à-vis to standard models. The mobility models proposed in literature have varying degrees of realism i.e. from random patterns to realistic patterns. Thus these models contribute significantly while testing the protocols for mobile ad hoc networks.
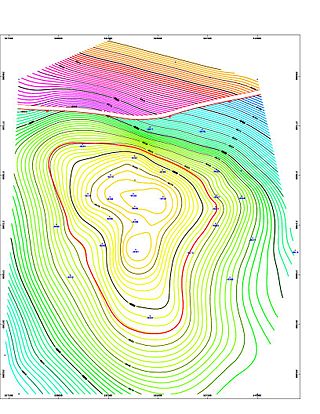
In the oil and gas industry, reservoir modeling involves the construction of a computer model of a petroleum reservoir, for the purposes of improving estimation of reserves and making decisions regarding the development of the field, predicting future production, placing additional wells and evaluating alternative reservoir management scenarios.

Traffic simulation or the simulation of transportation systems is the mathematical modeling of transportation systems through the application of computer software to better help plan, design, and operate transportation systems. Simulation of transportation systems started over forty years ago, and is an important area of discipline in traffic engineering and transportation planning today. Various national and local transportation agencies, academic institutions and consulting firms use simulation to aid in their management of transportation networks.
In mathematical modeling, deterministic simulations contain no random variables and no degree of randomness, and consist mostly of equations, for example difference equations. These simulations have known inputs and they result in a unique set of outputs. Contrast stochastic (probability) simulation, which includes random variables.
For pensions, a reliable Pension model is necessary for system simulations and projections, so it is important to have a sound database for pension system analyses. For an example of a complex pension model see e.g..
The Dynamic Microsimulation Model of the Czech Republic is a dynamic microsimulation pension model simulating the pension system of the Czech Republic, owned by the Ministry of Labour and Social Affairs.
Stochastic Process Rare Event Sampling (SPRES) is a Rare Event Sampling method in computer simulation, designed specifically for non-equilibrium calculations, including those for which the rare-event rates are time-dependent. To treat systems in which there is time dependence in the dynamics, due either to variation of an external parameter or to evolution of the system itself, the scheme for branching paths must be devised so as to achieve sampling which is distributed evenly in time and which takes account of changing fluxes through different regions of the phase space.



