 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages)
|
Equimolar counterdiffusion is an instance of molecular diffusion in a binary mixture, and occurs when equal numbers of molecules of the two substances are moving in opposite directions. [1] [2]
There are three different types of diffusion: molecular, Brownian and turbulent. Molecular diffusion occurs in gases, liquids, and solids. Diffusion is a result of thermal motion of molecules. Usually, convection occurs as a result of the diffusion process. The rate at which diffusion occurs depends on the state of the molecules: it occurs at a high rate in gases, a slower rate in liquids, and an even slower rate in solids. In gases, molecular diffusion is dependent on pressure and temperature. The higher the pressure, the slower the diffusion takes place, and the higher the temperature, the faster the diffusion takes place. In liquids, an increase in temperature increases the rate of diffusion. However, since liquids are incompressible, the rate of diffusion is not affected by the pressure. The rate of diffusion in solids is also increased by temperature.
Heat and mass transfer occurs from areas of higher concentration to areas of lower concentration. A simplistic way to picture diffusion is when ink is put on a paper towel; it spreads from areas of high concentration to areas of low concentration. The equation for this is shown below and is similar to the heat equation.
where
However, if a mixture is not of a pure concentration but consists of two species; then it is a binary flow, and the two flows must balance each other. This type of diffusion is referred to as equimolar counterdiffusion, and the two species, A and B, are in combination with each other. As an example, if there are two groups of mixtures containing species A and B connected by a channel, then species A will diffuse in the direction of species B, and vice versa. Specifically, for gases, assuming ideal gas behavior (P=CRuT), the molar concentration C will remain constant since the pressure and temperature are constant. Therefore, the molar flow rates of each species must be equal in magnitude and opposite in direction:
In this process, the net molar flow rate of the mixture and the molar-average velocity are equal to zero, and mass transfer occurs by diffusion only without any convection taking place.
The mole fraction, the molar concentration, and the partial pressure of both gases involved in equimolar counterdiffusion vary linearly. These relationships can be found in the following equations expressing the molar flow rates for each species, A and B, for a one-dimensional flow through a channel with no homogeneous chemical reactions:
where
We can use this equation to calculate the rate of diffusion in the surface of a catalyst thus: the mole fraction yB,1 is the concentration in the bulk fluid and the concentration yB,2 is the concentration of molecule B liquid at the surface of a catalyst. The diffusion in the bulk fluide compensate the utilisation of B at the surface of the catalyst. kg is the mass transfer coefficient.
Although the mixture is stationary due to the molar flow rate and velocity being zero, the net mass flow rate of the mixture is not equal to zero unless the molar mass of A is equal to the molar mass of B. The mass flow rate can be found using the following equation:
Molecular diffusion, often simply called diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a phase with uniform temperature, absent external net forces acting on the particles, the diffusion process will eventually result in complete mixing.
Evaporation is a type of vaporization that occurs on the surface of a liquid as it changes into the gas phase. A high concentration of the evaporating substance in the surrounding gas significantly slows down evaporation, such as when humidity affects rate of evaporation of water. When the molecules of the liquid collide, they transfer energy to each other based on how they collide. When a molecule near the surface absorbs enough energy to overcome the vapor pressure, it will escape and enter the surrounding air as a gas. When evaporation occurs, the energy removed from the vaporized liquid will reduce the temperature of the liquid, resulting in evaporative cooling.
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.
In chemistry, a solution is a special type of homogeneous mixture composed of two or more substances. In such a mixture, a solute is a substance dissolved in another substance, known as a solvent. If the attractive forces between the solvent and solute particles are greater than the attractive forces holding the solute particles together, the solvent particles pull the solute particles apart and surround them. These surrounded solute particles then move away from the solid solute and out into the solution. The mixing process of a solution happens at a scale where the effects of chemical polarity are involved, resulting in interactions that are specific to solvation. The solution usually has the state of the solvent when the solvent is the larger fraction of the mixture, as is commonly the case. One important parameter of a solution is the concentration, which is a measure of the amount of solute in a given amount of solution or solvent. The term "aqueous solution" is used when one of the solvents is water.
The volumetric heat capacity of a material is the heat capacity of a sample of the substance divided by the volume of the sample. It is the amount of energy that must be added, in the form of heat, to one unit of volume of the material in order to cause an increase of one unit in its temperature. The SI unit of volumetric heat capacity is joule per kelvin per cubic meter, J⋅K−1⋅m−3.
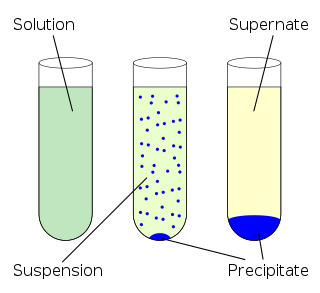
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. It treats a gas as composed of numerous particles, too small to see with a microscope, which are constantly in random motion. Their collisions with each other and with the walls of their container are used to explain physical properties of the gas—for example, the relationship between its temperature, pressure, and volume. The particles are now known to be the atoms or molecules of the gas.
In chemical thermodynamics, activity is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution. The term "activity" in this sense was coined by the American chemist Gilbert N. Lewis in 1907.
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is different from chemical thermodynamics, which deals with the direction in which a reaction occurs but in itself tells nothing about its rate. Chemical kinetics includes investigations of how experimental conditions influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition states, as well as the construction of mathematical models that also can describe the characteristics of a chemical reaction.
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of chemical equilibrium. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas.
Collision theory is a principle of chemistry used to predict the rates of chemical reactions. It states that when suitable particles of the reactant hit each other with the correct orientation, only a certain amount of collisions result in a perceptible or notable change; these successful changes are called successful collisions. The successful collisions must have enough energy, also known as activation energy, at the moment of impact to break the pre-existing bonds and form all new bonds. This results in the products of the reaction. The activation energy is often predicted using the Transition state theory. Increasing the concentration of the reactant brings about more collisions and hence more successful collisions. Increasing the temperature increases the average kinetic energy of the molecules in a solution, increasing the number of collisions that have enough energy. Collision theory was proposed independently by Max Trautz in 1916 and William Lewis in 1918.
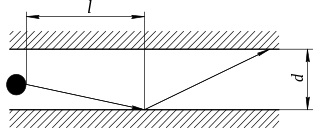
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore with a narrow diameter (2–50 nm) because molecules frequently collide with the pore wall. As another example, consider the diffusion of gas molecules through very small capillary pores. If the pore diameter is smaller than the mean free path of the diffusing gas molecules, and the density of the gas is low, the gas molecules collide with the pore walls more frequently than with each other, leading to Knudsen diffusion.
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry.
This glossary of chemistry terms is a list of terms and definitions relevant to chemistry, including chemical laws, diagrams and formulae, laboratory tools, glassware, and equipment. Chemistry is a physical science concerned with the composition, structure, and properties of matter, as well as the changes it undergoes during chemical reactions; it features an extensive vocabulary and a significant amount of jargon.
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus its SI units are newton-seconds per square meter, or pascal-seconds.
The Glossary of fuel cell terms lists the definitions of many terms used within the fuel cell industry. The terms in this fuel cell glossary may be used by fuel cell industry associations, in education material and fuel cell codes and standards to name but a few.
Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
Microvasculature comprises the microvessels – venules and capillaries of the microcirculation, with a maximum average diameter of 0.3 millimeters. As the vessels decrease in size, they increase their surface-area-to-volume ratio. This allows surface properties to play a significant role in the function of the vessel.
The physiology of decompression is the aspect of physiology which is affected by exposure to large changes in ambient pressure. It involves a complex interaction of gas solubility, partial pressures and concentration gradients, diffusion, bulk transport and bubble mechanics in living tissues. Gas is breathed at ambient pressure, and some of this gas dissolves into the blood and other fluids. Inert gas continues to be taken up until the gas dissolved in the tissues is in a state of equilibrium with the gas in the lungs, or the ambient pressure is reduced until the inert gases dissolved in the tissues are at a higher concentration than the equilibrium state, and start diffusing out again.
