
The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.

The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.
In two dimensions, the problem can be solved in polynomial time in a model of computation allowing addition and comparisons of real numbers, despite theoretical difficulties involving the numerical precision needed to perform such calculations. These algorithms are based on two different principles, either performing a shortest path algorithm such as Dijkstra's algorithm on a visibility graph derived from the obstacles or (in an approach called the continuous Dijkstra method) propagating a wavefront from one of the points until it meets the other.
In three (and higher) dimensions the problem is NP-hard in the general case, [1] but there exist efficient approximation algorithms that run in polynomial time based on the idea of finding a suitable sample of points on the obstacle edges and performing a visibility graph calculation using these sample points.
There are many results on computing shortest paths which stays on a polyhedral surface. Given two points s and t, say on the surface of a convex polyhedron, the problem is to compute a shortest path that never leaves the surface and connects s with t. This is a generalization of the problem from 2-dimension but it is much easier than the 3-dimensional problem.
There are variations of this problem, where the obstacles are weighted, i.e., one can go through an obstacle, but it incurs an extra cost to go through an obstacle. The standard problem is the special case where the obstacles have infinite weight. This is termed as the weighted region problem in the literature.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals and minimizes the total weight of its edges. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.
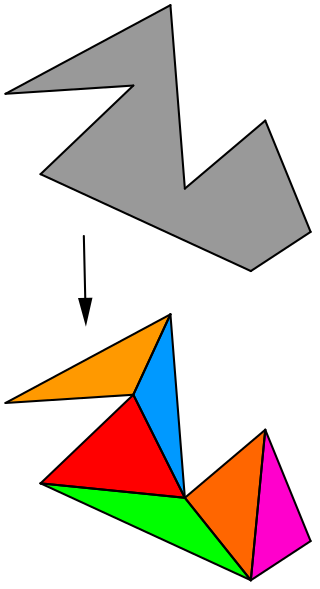
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them. That is, if the line segment connecting two locations does not pass through any obstacle, an edge is drawn between them in the graph. When the set of locations lies in a line, this can be understood as an ordered series. Visibility graphs have therefore been extended to the realm of time series analysis.
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:
"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

In geometry, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction as C at these points. That is, L is a tangent line at P and at Q.

In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.
In geometry, visibility is a mathematical abstraction of the real-life notion of visibility.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points and by an edge whenever there does not exist a third point that is closer to both and than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.
In mathematics, the Fréchet distance is a measure of similarity between curves that takes into account the location and ordering of the points along the curves. It is named after Maurice Fréchet.

Kenneth Lee Clarkson is an American computer scientist known for his research in computational geometry. He is a researcher at the IBM Almaden Research Center, and co-editor-in-chief of the Journal of Computational Geometry.

In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
John E. Hershberger is an American computer scientist and software professional, a principal engineer at Mentor Graphics Corporation since 1993. He is known for his research in computational geometry and algorithm engineering.
In distributed computing and geometric graph theory, greedy embedding is a process of assigning coordinates to the nodes of a telecommunications network in order to allow greedy geographic routing to be used to route messages within the network. Although greedy embedding has been proposed for use in wireless sensor networks, in which the nodes already have positions in physical space, these existing positions may differ from the positions given to them by greedy embedding, which may in some cases be points in a virtual space of a higher dimension, or in a non-Euclidean geometry. In this sense, greedy embedding may be viewed as a form of graph drawing, in which an abstract graph is embedded into a geometric space.

In computational geometry, a greedy geometric spanner is an undirected graph whose distances approximate the Euclidean distances among a finite set of points in a Euclidean space. The vertices of the graph represent these points. The edges of the spanner are selected by a greedy algorithm that includes an edge whenever its two endpoints are not connected by a short path of shorter edges. The greedy spanner was first described in the PhD thesis of Gautam Das and conference paper and subsequent journal paper by Ingo Althöfer et al. These sources also credited Marshall Bern (unpublished) with the independent discovery of the same construction.