External links
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
  | This biography of an Irish academic is a stub. You can help Wikipedia by expanding it. |
Eugene O'Riordan is an author and professor at the Dublin City University School of Mathematical Sciences, Dublin, Ireland. His areas of research include singularly perturbed differential equations, numerical analysis and Shishkin meshes. [1]
Books by Eugene O'Riordan include:
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
| | This biography of an Irish academic is a stub. You can help Wikipedia by expanding it. |
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.
Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics - an area of study which supplements both theory and experiment.
Computational science, also known as scientific computing, technical computing or scientific computation (SC), is an area of science that uses advanced computing capabilities to understand and solve complex physical problems. This includes
Computational Economics is an interdisciplinary research discipline that involves computer science, economics, and management science. This subject encompasses computational modeling of economic systems. Some of these areas are unique, while others established areas of economics by allowing robust data analytics and solutions of problems that would be arduous to research without computers and associated numerical methods.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.
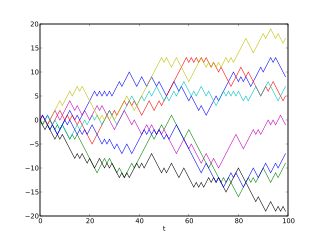
Computational finance is a branch of applied computer science that deals with problems of practical interest in finance. Some slightly different definitions are the study of data and algorithms currently used in finance and the mathematics of computer programs that realize financial models or systems.
Stanley Osher is an American mathematician, known for his many contributions in shock capturing, level-set methods, and PDE-based methods in computer vision and image processing. Osher is a professor at the University of California, Los Angeles (UCLA), Director of Special Projects in the Institute for Pure and Applied Mathematics (IPAM) and member of the California NanoSystems Institute (CNSI) at UCLA.
In mathematical economics, applied general equilibrium (AGE) models were pioneered by Herbert Scarf at Yale University in 1967, in two papers, and a follow-up book with Terje Hansen in 1973, with the aim of empirically estimating the Arrow–Debreu model of general equilibrium theory with empirical data, to provide "“a general method for the explicit numerical solution of the neoclassical model” (Scarf with Hansen 1973: 1)
Gene Howard Golub, was an American numerical analyst who taught at Stanford University as Fletcher Jones Professor of Computer Science and held a courtesy appointment in electrical engineering.
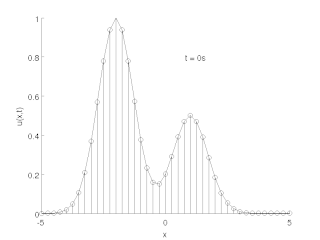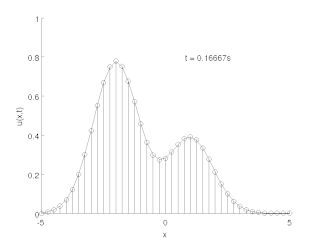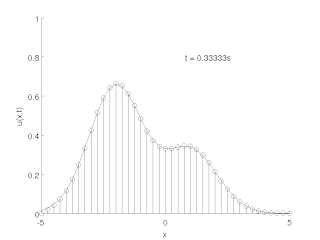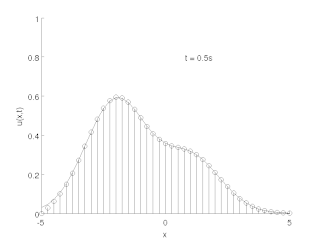
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.
Alexandre Joel Chorin is an American mathematician known for his contributions to computational fluid mechanics, turbulence, and computational statistical mechanics.
Computational mathematics is an area of mathematics devoted to the interaction between mathematics and computer computation.
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models.
João Arménio Correia Martins was born on November 11, 1951, at the southern town of Olhão in Portugal. He attended high school at the Liceu Nacional de Faro which he completed in 1969. Afterwards João Martins moved to Lisbon where he was graduate student of Civil Engineering at Instituto Superior Técnico (IST) until 1976. He was a research assistant and assistant instructor at IST until 1981. Subsequently, he entered the graduate school in the College of Engineering, Department of Aerospace Engineering and Engineering Mechanics of The University of Texas at Austin, USA. There he obtained a MSc in 1983 with a thesis titled A Numerical Analysis of a Class of Problems in Elastodynamics with Friction Effects and a PhD in 1986 with a thesis titled Dynamic Frictional Contact Problems Involving Metallic Bodies, both supervised by Prof. John Tinsley Oden. He returned to Portugal in 1986 and became assistant professor at IST. In 1989 he became associate professor and in 1996 he earned the academic degree of “agregado” from Universidade Técnica de Lisboa. Later, in 2005, he became full professor in the Department of Civil Engineering and Architecture of IST.
The following is a timeline of scientific computing, also known as computational science.
In mathematics, specifically in computational geometry, geometric nonrobustness is a problem wherein branching decisions in computational geometry algorithms are based on approximate numerical computations, leading to various forms of unreliability including ill-formed output and software failure through crashing or infinite loops.
Sara Zahedi is an Iranian-Swedish mathematician who works in computational fluid dynamics and holds an associate professorship in numerical analysis at the Royal Institute of Technology (KTH) in Sweden. She is one of ten winners and the only female winner of the European Mathematical Society Prize for 2016 "for her outstanding research regarding the development and analysis of numerical algorithms for partial differential equations with a focus on applications to problems with dynamically changing geometry". The topic of Zahedi's EMS Prize lecture was her recent research on the CutFEM method of solving fluid dynamics problems with changing boundary geometry, such as arise when simulating the dynamics of systems of two immiscible liquids. This method combines level set methods to represent the domain boundaries as cuts through an underlying uniform grid, together with numerical simulation techniques that can adapt to the complex geometries of grid cells cut by these boundaries.
Beatrice Meini is an Italian computational mathematician and numerical analyst specializing in numerical linear algebra and its applications to Markov chains, matrix equations, and queueing theory. She is Professor of Numerical Analysis in the Department of Mathematics at the University of Pisa.