
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. That is, it is a k-ary tree with k = 2. A recursive definition using set theory is that a binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
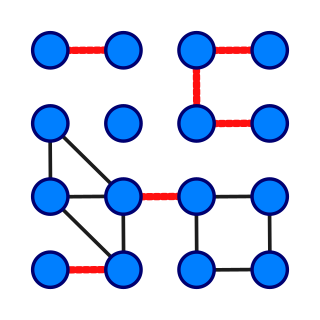
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

In graph theory, a biconnected component or block is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block-cut tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or separating vertices or articulation points. Specifically, a cut vertex is any vertex whose removal increases the number of connected components. A block containing at most one cut vertex is called a leaf block, it corresponds to a leaf vertex in the block-cut tree.
In parallel algorithms, the list ranking problem involves determining the position, or rank, of each item in a linked list. That is, the first item in the list should be assigned the number 1, the second item in the list should be assigned the number 2, etc. Although it is straightforward to solve this problem efficiently on a sequential computer, by traversing the list in order, it is more complicated to solve in parallel. As Anderson & Miller (1990) wrote, the problem was viewed as important in the parallel algorithms community both for its many applications and because solving it led to many important ideas that could be applied in parallel algorithms more generally.
In computer science, the prefix sum, cumulative sum, inclusive scan, or simply scan of a sequence of numbers x0, x1, x2, ... is a second sequence of numbers y0, y1, y2, ..., the sums of prefixes of the input sequence:
In graph theory and computer science, the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest node that has both v and w as descendants, where we define each node to be a descendant of itself.
A link/cut tree is a data structure for representing a forest, a set of rooted trees, and offers the following operations:

In graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and more specifically graph algorithms, to represent the triconnected components of a graph. The SPQR tree of a graph may be constructed in linear time and has several applications in dynamic graph algorithms and graph drawing.
In computer science, a finger tree is a purely functional data structure that can be used to efficiently implement other functional data structures. A finger tree gives amortized constant time access to the "fingers" (leaves) of the tree, which is where data is stored, and concatenation and splitting logarithmic time in the size of the smaller piece. It also stores in each internal node the result of applying some associative operation to its descendants. This "summary" data stored in the internal nodes can be used to provide the functionality of data structures other than trees.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.

A Fenwick tree or binary indexed tree(BIT) is a data structure that can efficiently update values and calculate prefix sums in an array of values.
Capacitated minimum spanning tree is a minimal cost spanning tree of a graph that has a designated root node and satisfies the capacity constraint . The capacity constraint ensures that all subtrees incident on the root node have no more than nodes. If the tree nodes have weights, then the capacity constraint may be interpreted as follows: the sum of weights in any subtree should be no greater than . The edges connecting the subgraphs to the root node are called gates. Finding the optimal solution is NP-hard.
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.
In graph theory and theoretical computer science, the level ancestor problem is the problem of preprocessing a given rooted tree T into a data structure that can determine the ancestor of a given node at a given distance from the root of the tree.
In computing and graph theory, a dynamic connectivity structure is a data structure that dynamically maintains information about the connected components of a graph.
In computer science, parallel tree contraction is a broadly applicable technique for the parallel solution of a large number of tree problems, and is used as an algorithm design technique for the design of a large number of parallel graph algorithms. Parallel tree contraction was introduced by Gary L. Miller and John H. Reif, and has subsequently been modified to improve efficiency by X. He and Y. Yesha, Hillel Gazit, Gary L. Miller and Shang-Hua Teng and many others.







