
In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends.
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals. Originally, they arose in connection with the problem of finding the arc length of an ellipse and were first studied by Giulio Fagnano and Leonhard Euler. Modern mathematics defines an "elliptic integral" as any function f which can be expressed in the form
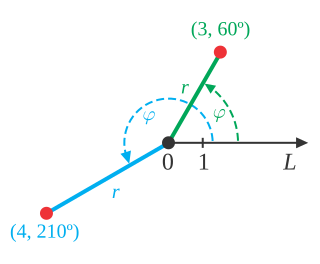
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t. Angles in polar notation are generally expressed in either degrees or radians.
In mechanics and physics, simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. It results in an oscillation which, if uninhibited by friction or any other dissipation of energy, continues indefinitely.
In complex analysis, an elliptic function is a meromorphic function that is periodic in two directions. Just as a periodic function of a real variable is defined by its values on an interval, an elliptic function is determined by its values on a fundamental parallelogram, which then repeat in a lattice. Such a doubly periodic function cannot be holomorphic, as it would then be a bounded entire function, and by Liouville's theorem every such function must be constant. In fact, an elliptic function must have at least two poles in a fundamental parallelogram, as it is easy to show using the periodicity that a contour integral around its boundary must vanish, implying that the residues of all simple poles must cancel.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.

Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that are of historical importance. They are found in the description of the motion of a pendulum, as well as in the design of the electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation sn for sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829).
The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was rather a set of heuristic corrections to classical mechanics. The theory is now understood as the semi-classical approximation to modern quantum mechanics.

In general relativity, Schwarzschild geodesics describe the motion of particles of infinitesimal mass in the gravitational field of a central fixed mass . Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System, and of the deflection of light by gravity.

In algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial
In physics, the Green's function for Laplace's equation in three variables is used to describe the response of a particular type of physical system to a point source. In particular, this Green's function arises in systems that can be described by Poisson's equation, a partial differential equation (PDE) of the form

The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation.
In classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:
In applied mathematics, discontinuous Galerkin methods form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics.
Landen's transformation is a mapping of the parameters of an elliptic integral, useful for the efficient numerical evaluation of elliptic functions. It was originally due to John Landen and independently rediscovered by Carl Friedrich Gauss.
In classical potential theory, the central-force problem is to determine the motion of a particle in a single central potential field. A central force is a force that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.







