 | This article relies largely or entirely on a single source .(April 2024) |
In mathematics, the Fatou conjecture, named after Pierre Fatou, states that a quadratic family of maps from the complex plane to itself is hyperbolic for an open dense set of parameters.
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.
In the mathematical field of geometric topology, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.
The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence. The conjecture has been shown to hold for all positive integers up to 2.95×1020, but no general proof has been found.
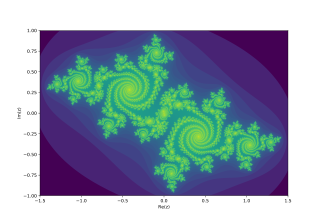
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".
Grigori Yakovlevich Perelman is a Russian mathematician who is known for his contributions to the fields of geometric analysis, Riemannian geometry, and geometric topology. In 2005, Perelman abruptly quit his research job at the Steklov Institute of Mathematics, and in 2006 stated that he had quit professional mathematics, due to feeling disappointed over the ethical standards in the field. He lives in seclusion in Saint Petersburg, and has not accepted offers for interviews since 2006.
Ludwig Georg Elias Moses Bieberbach was a German mathematician and Nazi.
Pierre Joseph Louis Fatou was a French mathematician and astronomer. He is known for major contributions to several branches of analysis. The Fatou lemma and the Fatou set are named after him.
Richard Lawrence Taylor is a British mathematician working in the field of number theory. He is currently the Barbara Kimball Browning Professor in Humanities and Sciences at Stanford University.
Thomas Hartwig Wolff was an American mathematician, working primarily in the fields of harmonic analysis, complex analysis, and partial differential equations. As an undergraduate at Harvard University, he regularly played poker with his classmate Bill Gates. While a graduate student at the University of California, Berkeley from 1976 to 1979, under the direction of Donald Sarason, he obtained a new proof of the corona theorem, a famously difficult theorem in complex analysis. He was made Professor of Mathematics at Caltech in 1986, and was there from 1988–1992 and from 1995 to his death in a car accident in 2000. He also held positions at the University of Washington, University of Chicago, New York University, and University of California, Berkeley.
Mitsuhiro Shishikura is a Japanese mathematician working in the field of complex dynamics. He is professor at Kyoto University in Japan.
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class.
In mathematics, a Fatou–Bieberbach domain is a proper subdomain of , biholomorphically equivalent to . That is, an open set is called a Fatou–Bieberbach domain if there exists a bijective holomorphic function whose inverse function is holomorphic. It is well-known that the inverse can not be polynomial.
In mathematics, the no-wandering-domain theorem is a result on dynamical systems, proven by Dennis Sullivan in 1985.
A Siegel disc or Siegel disk is a connected component in the Fatou set where the dynamics is analytically conjugate to an irrational rotation.
Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Part of the inspiration comes from complex dynamics, the study of the iteration of self-maps of the complex plane or other complex algebraic varieties. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in 2000. The Clay Institute has pledged a US$1 million prize for the first correct solution to each problem.
In mathematics, and particularly complex dynamics, the escaping set of an entire function ƒ consists of all points that tend to infinity under the repeated application of ƒ. That is, a complex number belongs to the escaping set if and only if the sequence defined by converges to infinity as gets large. The escaping set of is denoted by .
Grzegorz Świątek is a Polish mathematician, currently a professor at the Warsaw University of Technology. He is known for his contributions to dynamical systems.
 | This mathematics-related article is a stub. You can help Wikipedia by expanding it. |