In differential geometry, flat map is a mapping that converts vectors into corresponding 1-forms, given a non-degenerate (0,2)-tensor.
In differential geometry, flat map is a mapping that converts vectors into corresponding 1-forms, given a non-degenerate (0,2)-tensor.
flatMap in functional programmingIn mathematics, any vector space has a corresponding dual vector space consisting of all linear forms on together with the vector space structure of pointwise addition and scalar multiplication by constants.
In mathematics, and more specifically in linear algebra, a linear map is a mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism.

A map is a symbolic depiction emphasizing relationships between elements of some space, such as objects, regions, or themes.
In mathematics, an operator is generally a mapping or function that acts on elements of a space to produce elements of another space. There is no general definition of an operator, but the term is often used in place of function when the domain is a set of functions or other structured objects. Also, the domain of an operator is often difficult to characterize explicitly, and may be extended so as to act on related objects. See Operator (physics) for other examples.

In Euclidean geometry, an affine transformation or affinity is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
Perceptual mapping or market mapping is a diagrammatic technique used by asset marketers that attempts to visually display the perceptions of customers or potential customers. The positioning of a brand is influenced by customer perceptions rather than by those of businesses. For example, a business may feel it sells upmarket products of high quality, but if customers view the products as low quality, it is their views which will influence sales. Typically the position of a company's product, product line, or brand is displayed relative to their competition. Perceptual maps, also known as market maps, usually have two dimensions but can be multi-dimensional or use multiple colours to add an extra variable. They can be used to identify gaps in the market and potential partners or merger targets as well as to clarify perceptual problems with a company's product. So, if a business wants to find out where its brand is positioned in the market, it might carry out market research. This will help them to find out how the customers sees their brand in relation to others in the market.

In mathematics, and particularly topology, a fiber bundle is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space and a product space is defined using a continuous surjective map, that in small regions of behaves just like a projection from corresponding regions of to The map called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space is known as the total space of the fiber bundle, as the base space, and the fiber.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. Affine space is the setting for affine geometry.
This is an outline of topics related to linear algebra, the branch of mathematics concerning linear equations and linear maps and their representations in vector spaces and through matrices.

In 3D computer graphics, normal mapping, or Dot3 bump mapping, is a texture mapping technique used for faking the lighting of bumps and dents – an implementation of bump mapping. It is used to add details without using more polygons. A common use of this technique is to greatly enhance the appearance and details of a low polygon model by generating a normal map from a high polygon model or height map.
In mathematics, a bilinear form is a bilinear map V × V → K on a vector space V over a field K. In other words, a bilinear form is a function B : V × V → K that is linear in each argument separately:
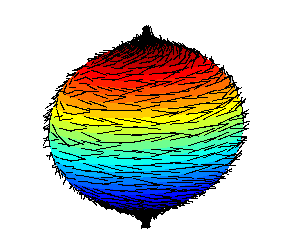
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional n-spheres. For the ordinary sphere, or 2‑sphere, if f is a continuous function that assigns a vector in R3 to every point p on a sphere such that f(p) is always tangent to the sphere at p, then there is at least one pole, a point where the field vanishes (a p such that f(p) = 0).
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G. It was much used by Élie Cartan as a basic ingredient of his method of moving frames, and bears his name together with that of Ludwig Maurer.
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a principal G-subbundle of the tangent frame bundle FM (or GL(M)) of M.

In computer graphics, cube mapping is a method of environment mapping that uses the six faces of a cube as the map shape. The environment is projected onto the sides of a cube and stored as six square textures, or unfolded into six regions of a single texture.
In mathematics, a versor is a quaternion of norm one. Each versor has the form

In computer graphics, a heightmap or heightfield is a raster image used mainly as Discrete Global Grid in secondary elevation modeling. Each pixel stores values, such as surface elevation data, for display in 3D computer graphics. A heightmap can be used in bump mapping to calculate where this 3D data would create shadow in a material, in displacement mapping to displace the actual geometric position of points over the textured surface, or for terrain where the heightmap is converted into a 3D mesh.
In differential geometry, the sharp map is the mapping that converts 1-forms into corresponding vectors, given a non-degenerate (0,2)-tensor.
Conformal geometric algebra (CGA) is the geometric algebra constructed over the resultant space of a map from points in an n-dimensional base space Rp,q to null vectors in Rp+1,q+1. This allows operations on the base space, including reflections, rotations and translations to be represented using versors of the geometric algebra; and it is found that points, lines, planes, circles and spheres gain particularly natural and computationally amenable representations.
This is a glossary of terms relating to computer graphics.