
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, these are the groups that obey the axiom of commutativity. Abelian groups generalize the arithmetic of addition of integers. They are named after early 19th century mathematician Niels Henrik Abel.

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined, and behave as the corresponding operations on rational and real numbers do.
A field is thus a fundamental algebraic structure, which is widely used in algebra, number theory and many other areas of mathematics.

In mathematics, a set B of elements (vectors) in a vector space V is called a basis, if every element of V may be written in a unique way as a (finite) linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates on B of the vector. The elements of a basis are called basis vectors.

In mathematics, a group is a set equipped with a binary operation which combines any two elements to form a third element in such a way that four conditions called group axioms are satisfied, namely closure, associativity, identity and invertibility. One of the most familiar examples of a group is the set of integers together with the addition operation, but groups are encountered in numerous areas within and outside mathematics, and help focusing on essential structural aspects, by detaching them from the concrete nature of the subject of the study.

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and order matters. Formally, a sequence can be defined as a function whose domain is either the set of the natural numbers or the set of the first n natural numbers. The position of an element in a sequence is its rank or index; it is the natural number from which the element is the image. It depends on the context or a specific convention, if the first element has index 0 or 1. When a symbol has been chosen for denoting a sequence, the nth element of the sequence is denoted by this symbol with n as subscript; for example, the nth element of the Fibonacci sequence is generally denoted Fn.

In mathematics, a ring is one of the fundamental algebraic structures used in abstract algebra. It consists of a set equipped with two binary operations that generalize the arithmetic operations of addition and multiplication. Through this generalization, theorems from arithmetic are extended to non-numerical objects such as polynomials, series, matrices and functions.
In mathematics, a formal power series is a generalization of a polynomial, where the number of terms is allowed to be infinite; this implies giving up the possibility of replacing the variable in the polynomial with an arbitrary number. Thus a formal power series differs from a polynomial in that it may have infinitely many terms, and differs from a power series, whose variables can take on numerical values. One way to view a formal power series is as an infinite ordered sequence of numbers. In this case, the powers of the variable are used only to indicate the order of the coefficients, so that the coefficient of
is the fifth term in the sequence. In combinatorics, formal power series provide representations of numerical sequences and of multisets, and for instance allow concise expressions for recursively defined sequences regardless of whether the recursion can be explicitly solved; this is known as the method of generating functions. More generally, formal power series can include series with any finite number of variables, and with coefficients in an arbitrary ring. Formal power series can be created from Taylor polynomials using formal moduli.
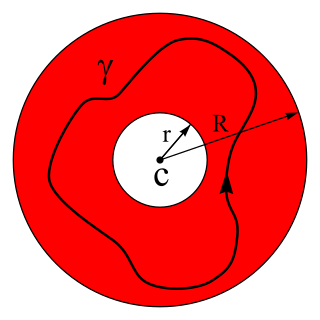
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.
In mathematics, a Laurent polynomial in one variable over a field
is a linear combination of positive and negative powers of the variable with coefficients in
. Laurent polynomials in X form a ring denoted
[X, X−1]. They differ from ordinary polynomials in that they may have terms of negative degree. The construction of Laurent polynomials may be iterated, leading to the ring of Laurent polynomials in several variables. Laurent polynomials are of particular importance in the study of complex variables.
In mathematics, a module is one of the fundamental algebraic structures used in abstract algebra. A module over a ring is a generalization of the notion of vector space over a field, wherein the corresponding scalars are the elements of an arbitrary given ring and a multiplication is defined between elements of the ring and elements of the module.

In abstract algebra, a finite group is a mathematical group with a finite number of elements. A group is a set of elements together with an operation which associates, to each ordered pair of elements, an element of the set. In the case of a finite group, the set is finite.
In mathematics, a free module is a module that has a basis – that is, a generating set consisting of linearly independent elements. Every vector space is a free module, but, if the ring of the coefficients is not a division ring, then there exist non-free modules.
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.
Abstract analytic number theory is a branch of mathematics which takes the ideas and techniques of classical analytic number theory and applies them to a variety of different mathematical fields. The classical prime number theorem serves as a prototypical example, and the emphasis is on abstract asymptotic distribution results. The theory was invented and developed by mathematicians such as John Knopfmacher and Arne Beurling in the twentieth century.
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of abelian groups and commutative semigroups with an operation of addition. Additive number theory has close ties to combinatorial number theory and the geometry of numbers. Two principal objects of study are the sumset of two subsets A and B of elements from an abelian group G,
In mathematics, an algebraic number field F is a finite degree field extension of the field of rational numbers Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space over Q.







