In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.

In calculus, Taylor's theorem gives an approximation of a -times differentiable function around a given point by a polynomial of degree , called the -th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.
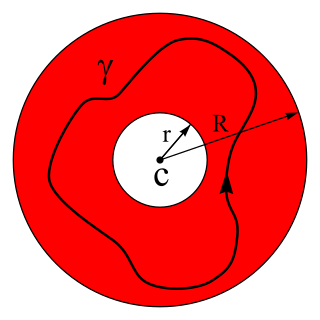
In mathematics, the Laurent series of a complex function is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function, the radius of convergence is the shortest or minimum of all the respective distances calculated from the center of the disk of convergence to the respective singularities of the function.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange–Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function. Lagrange inversion is a special case of the inverse function theorem.
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In mathematics, a Dirichlet series is any series of the form
In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like for a nonnegative integer . Specifically, the binomial series is the MacLaurin series for the function , where and . Explicitly,
In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin-Louis Cauchy.
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence defines a series S that is denoted
In mathematics, Borel summation is a summation method for divergent series, introduced by Émile Borel. It is particularly useful for summing divergent asymptotic series, and in some sense gives the best possible sum for such series. There are several variations of this method that are also called Borel summation, and a generalization of it called Mittag-Leffler summation.

In mathematics, Puiseux series are a generalization of power series that allow for negative and fractional exponents of the indeterminate. For example, the series
In real analysis and complex analysis, branches of mathematics, the identity theorem for analytic functions states: given functions f and g analytic on a domain D, if f = g on some , where has an accumulation point in D, then f = g on D.
In mathematics, Abel's test is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Henrik Abel, who proved it in 1826. There are two slightly different versions of Abel's test – one is used with series of real numbers, and the other is used with power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters.
In mathematics, for a sequence of complex numbers a1, a2, a3, ... the infinite product
In analytic number theory, a Dirichlet series, or Dirichlet generating function (DGF), of a sequence is a common way of understanding and summing arithmetic functions in a meaningful way. A little known, or at least often forgotten about, way of expressing formulas for arithmetic functions and their summatory functions is to perform an integral transform that inverts the operation of forming the DGF of a sequence. This inversion is analogous to performing an inverse Z-transform to the generating function of a sequence to express formulas for the series coefficients of a given ordinary generating function.




















































































