In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions:

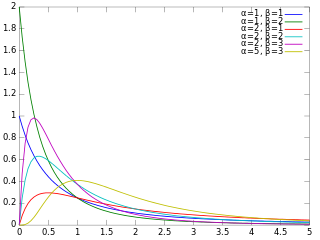
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by alpha (α) and beta (β), that appear as exponents of the random variable and control the shape of the distribution. The generalization to multiple variables is called a Dirichlet distribution.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.

In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.
In mathematics, a generalized hypergeometric series is a power series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by analytic continuation. The generalized hypergeometric series is sometimes just called the hypergeometric series, though this term also sometimes just refers to the Gaussian hypergeometric series. Generalized hypergeometric functions include the (Gaussian) hypergeometric function and the confluent hypergeometric function as special cases, which in turn have many particular special functions as special cases, such as elementary functions, Bessel functions, and the classical orthogonal polynomials.
In numerical analysis, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.

In probability and statistics, the Dirichlet distribution, often denoted , is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, hence its alternative name of multivariate beta distribution (MBD). Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
In mathematics, Riemann's differential equation, named after Bernhard Riemann, is a generalization of the hypergeometric differential equation, allowing the regular singular points to occur anywhere on the Riemann sphere, rather than merely at 0, 1, and . The equation is also known as the Papperitz equation.
In mathematics, basic hypergeometric series, or q-hypergeometric series, are q-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution.
In mathematics, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
A quasiprobability distribution is a mathematical object similar to a probability distribution but which relaxes some of Kolmogorov's axioms of probability theory. Quasiprobabilities share several of general features with ordinary probabilities, such as, crucially, the ability to yield expectation values with respect to the weights of the distribution. They can however violate the σ-additivity axiom: integrating them over does not necessarily yield probabilities of mutually exclusive states. Indeed, quasiprobability distributions also counterintuitively have regions of negative probability density, contradicting the first axiom. Quasiprobability distributions arise naturally in the study of quantum mechanics when treated in phase space formulation, commonly used in quantum optics, time-frequency analysis, and elsewhere.

In directional statistics, the Kent distribution, also known as the 5-parameter Fisher–Bingham distribution, is a probability distribution on the unit sphere. It is the analogue on S2 of the bivariate normal distribution with an unconstrained covariance matrix. The Kent distribution was proposed by John T. Kent in 1982, and is used in geology as well as bioinformatics.
In mathematics, the Jack function is a generalization of the Jack polynomial, introduced by Henry Jack. The Jack polynomial is a homogeneous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by the Heckman–Opdam polynomials and Macdonald polynomials.
In statistics, the generalized Dirichlet distribution (GD) is a generalization of the Dirichlet distribution with a more general covariance structure and almost twice the number of parameters. Random variables with a GD distribution are not completely neutral.
In statistics, the matrix t-distribution is the generalization of the multivariate t-distribution from vectors to matrices. The matrix t-distribution shares the same relationship with the multivariate t-distribution that the matrix normal distribution shares with the multivariate normal distribution. For example, the matrix t-distribution is the compound distribution that results from sampling from a matrix normal distribution having sampled the covariance matrix of the matrix normal from an inverse Wishart distribution.
In mathematics, the Romanovski polynomials are one of three finite subsets of real orthogonal polynomials discovered by Vsevolod Romanovsky within the context of probability distribution functions in statistics. They form an orthogonal subset of a more general family of little-known Routh polynomials introduced by Edward John Routh in 1884. The term Romanovski polynomials was put forward by Raposo, with reference to the so-called 'pseudo-Jacobi polynomials in Lesky's classification scheme. It seems more consistent to refer to them as Romanovski–Routh polynomials, by analogy with the terms Romanovski–Bessel and Romanovski–Jacobi used by Lesky for two other sets of orthogonal polynomials.