The number e is a mathematical constant, approximately equal to 2.71828, that is the base of the natural logarithm. It can be calculated as is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the computation of compound interest, or as the sum of the infinite series
In mathematics, the Euler–Maclaurin formula is a formula for the difference between an integral and a closely related sum. It can be used to approximate integrals by finite sums, or conversely to evaluate finite sums and infinite series using integrals and the machinery of calculus. For example, many asymptotic expansions are derived from the formula, and Faulhaber's formula for the sum of powers is an immediate consequence.

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,
In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

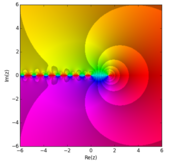
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as

In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.

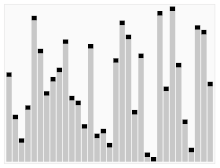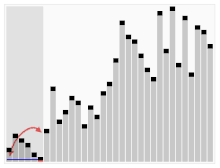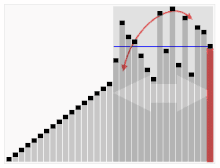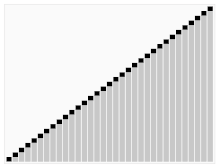
Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In probability theory, the law of large numbers (LLN) is a mathematical theorem that states that the average of the results obtained from a large number of independent and identical random samples converges to the true value, if it exists. More formally, the LLN states that given a sample of independent and identically distributed values, the sample mean converges to the true mean.

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

The sum of the reciprocals of all prime numbers diverges; that is:

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, the integral test for convergence is a method used to test infinite series of monotonous terms for convergence. It was developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, an alternating series is an infinite series of the form
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.
In mathematics, the Leibniz formula for π, named after Gottfried Wilhelm Leibniz, states that
In mathematics, the Riemann series theorem, also called the Riemann rearrangement theorem, named after 19th-century German mathematician Bernhard Riemann, says that if an infinite series of real numbers is conditionally convergent, then its terms can be arranged in a permutation so that the new series converges to an arbitrary real number, or diverges. This implies that a series of real numbers is absolutely convergent if and only if it is unconditionally convergent.
In mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving gamma functions and zeta functions. It is named after mathematicians James Whitbread Lee Glaisher and Hermann Kinkelin.
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation