Trigonometric substitution

In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. ^{[1] [2]} Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.

Case I: Integrands containing a² − x²

Let ${\displaystyle x=a\sin \theta ,}$ and use the identity ${\displaystyle 1-\sin ^{2}\theta =\cos ^{2}\theta .}$

Examples of Case I

Geometric construction for Case I

Example 1

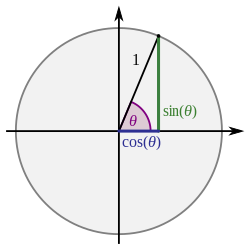
In the integral

$${\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},}$$

we may use

$${\displaystyle x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.}$$

Then, $${\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}$$

The above step requires that ${\displaystyle a>0}$ and ${\displaystyle \cos \theta >0.}$ We can choose ${\displaystyle a}$ to be the principal root of ${\displaystyle a^{2},}$ and impose the restriction ${\displaystyle -\pi /2<\theta <\pi /2}$ by using the inverse sine function.

For a definite integral, one must figure out how the bounds of integration change. For example, as ${\displaystyle x}$ goes from ${\displaystyle 0}$ to ${\displaystyle a/2,}$ then ${\displaystyle \sin \theta }$ goes from ${\displaystyle 0}$ to ${\displaystyle 1/2,}$ so ${\displaystyle \theta }$ goes from ${\displaystyle 0}$ to ${\displaystyle \pi /6.}$ Then,

$${\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.}$$

Some care is needed when picking the bounds. Because integration above requires that ${\displaystyle -\pi /2<\theta <\pi /2}$ , ${\displaystyle \theta }$ can only go from ${\displaystyle 0}$ to ${\displaystyle \pi /6.}$ Neglecting this restriction, one might have picked ${\displaystyle \theta }$ to go from ${\displaystyle \pi }$ to ${\displaystyle 5\pi /6,}$ which would have resulted in the negative of the actual value.

Alternatively, fully evaluate the indefinite integrals before applying the boundary conditions. In that case, the antiderivative gives

$${\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}}$$ as before.

Example 2

The integral

$${\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx,}$$

may be evaluated by letting ${\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\dfrac {x}{a}},}$ where ${\displaystyle a>0}$ so that ${\textstyle {\sqrt {a^{2}}}=a,}$ and ${\textstyle -\pi /2\leq \theta \leq \pi /2}$ by the range of arcsine, so that ${\displaystyle \cos \theta \geq 0}$ and ${\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .}$

Then, $${\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}$$

For a definite integral, the bounds change once the substitution is performed and are determined using the equation ${\textstyle \theta =\arcsin {\dfrac {x}{a}},}$ with values in the range ${\textstyle -\pi /2\leq \theta \leq \pi /2.}$ Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

$${\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,}$$

may be evaluated by substituting ${\displaystyle x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,}$ with the bounds determined using ${\textstyle \theta =\arcsin {\dfrac {x}{2}}.}$

Because ${\displaystyle \arcsin(1/{2})=\pi /6}$ and ${\displaystyle \arcsin(-1/2)=-\pi /6,}$$${\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}$$

On the other hand, direct application of the boundary terms to the previously obtained formula for the antiderivative yields $${\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[{\frac {2^{2}}{2}}\arcsin {\frac {x}{2}}+{\frac {x}{2}}{\sqrt {2^{2}-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}$$ as before.

Case II: Integrands containing a² + x²

Let ${\displaystyle x=a\tan \theta ,}$ and use the identity ${\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta .}$

Examples of Case II

Geometric construction for Case II

Example 1

In the integral

$${\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}}$$

we may write

$${\displaystyle x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},}$$

so that the integral becomes

$${\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\[6pt]&=\int {\frac {d\theta }{a}}\\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}}$$

provided ${\displaystyle a\neq 0.}$

For a definite integral, the bounds change once the substitution is performed and are determined using the equation ${\displaystyle \theta =\arctan {\frac {x}{a}},}$ with values in the range ${\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.}$ Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

$${\displaystyle \int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,}$$

may be evaluated by substituting ${\displaystyle x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,}$ with the bounds determined using ${\displaystyle \theta =\arctan x.}$

Since ${\displaystyle \arctan 0=0}$ and ${\displaystyle \arctan 1=\pi /4,}$$${\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}$$

Meanwhile, direct application of the boundary terms to the formula for the antiderivative yields $${\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\left[{\frac {1}{1}}\arctan {\frac {x}{1}}\right]_{0}^{1}\\[6pt]&=4(\arctan x){\Bigg |}_{0}^{1}\\[6pt]&=4(\arctan 1-\arctan 0)\\[6pt]&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}$$ same as before.

Example 2

The integral

$${\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}}$$

may be evaluated by letting ${\displaystyle x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},}$

where ${\displaystyle a>0}$ so that ${\displaystyle {\sqrt {a^{2}}}=a,}$ and ${\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}}$ by the range of arctangent, so that ${\displaystyle \sec \theta >0}$ and ${\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta .}$

Then, $${\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}$$ The integral of secant cubed may be evaluated using integration by parts. As a result, $${\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}$$

Case III: Integrands containing x² − a²

Let ${\displaystyle x=a\sec \theta ,}$ and use the identity ${\displaystyle \sec ^{2}\theta -1=\tan ^{2}\theta .}$

Examples of Case III

Geometric construction for Case III

Integrals such as

$${\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}}$$

can also be evaluated by partial fractions rather than trigonometric substitutions. However, the integral

$${\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx}$$

cannot. In this case, an appropriate substitution is: $${\displaystyle x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}$$

where ${\displaystyle a>0}$ so that ${\displaystyle {\sqrt {a^{2}}}=a,}$ and ${\displaystyle 0\leq \theta <{\frac {\pi }{2}}}$ by assuming ${\displaystyle x>0,}$ so that ${\displaystyle \tan \theta \geq 0}$ and ${\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta .}$

Then, $${\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}}$$

One may evaluate the integral of the secant function by multiplying the numerator and denominator by ${\displaystyle (\sec \theta +\tan \theta )}$ and the integral of secant cubed by parts. ^[3] As a result, $${\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}$$

When ${\displaystyle {\frac {\pi }{2}}<\theta \leq \pi ,}$ which happens when ${\displaystyle x<0}$ given the range of arcsecant, ${\displaystyle \tan \theta \leq 0,}$ meaning ${\displaystyle {\sqrt {\tan ^{2}\theta }}=-\tan \theta }$ instead in that case.

Substitutions that eliminate trigonometric functions

Substitution can be used to remove trigonometric functions.

For instance,

$${\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\frac {x}{2}}\right)\\[6pt]\end{aligned}}}$$

The last substitution is known as the Weierstrass substitution, which makes use of tangent half-angle formulas.

For example,

$${\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}}$$

Hyperbolic substitution

Substitutions of hyperbolic functions can also be used to simplify integrals. ^[4]

For example, to integrate ${\displaystyle 1/{\sqrt {a^{2}+x^{2}}}}$, introduce the substitution ${\displaystyle x=a\sinh {u}}$ (and hence ${\displaystyle dx=a\cosh u\,du}$), then use the identity ${\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1}$ to find:

$${\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\\[6pt]&=\int {\frac {\cosh {u}\,du}{\sqrt {1+\sinh ^{2}{u}}}}\\[6pt]&=\int {\frac {\cosh {u}}{\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C.\end{aligned}}}$$

If desired, this result may be further transformed using other identities, such as using the relation ${\displaystyle \sinh ^{-1}{z}=\operatorname {arsinh} {z}=\ln(z+{\sqrt {z^{2}+1}})}$: $${\displaystyle {\begin{aligned}\sinh ^{-1}{\frac {x}{a}}+C&=\ln \left({\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}+1}}\,\right)+C\\[6pt]&=\ln \left({\frac {x+{\sqrt {x^{2}+a^{2}}}}{a}}\,\right)+C.\end{aligned}}}$$

See also

• Mathematics portal

• Integration by substitution
• Weierstrass substitution
• Euler substitution

References

1. Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN   978-0-495-01166-8.
2. Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN   978-0-321-58876-0.
3. Stewart, James (2012). "Section 7.2: Trigonometric Integrals". Calculus - Early Transcendentals. United States: Cengage Learning. pp. 475–6. ISBN   978-0-538-49790-9.
4. Boyadzhiev, Khristo N. "Hyperbolic Substitutions for Integrals" (PDF). Archived from the original (PDF) on 26 February 2020. Retrieved 4 March 2013.