
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration started as a method to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Today integration is used in a wide variety of scientific fields.

In physics and mathematics, the Fourier transform (FT) is a transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into terms of the intensity of its constituent pitches.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.

In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.

In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line that lies on the same plane. The surface created by this revolution and which bounds the solid is the surface of revolution.

A surface of revolution is a surface in Euclidean space created by rotating a curve one full revolution around an axis of rotation.

Shell integration is a method for calculating the volume of a solid of revolution, when integrating along an axis perpendicular to the axis of revolution. This is in contrast to disc integration which integrates along the axis parallel to the axis of revolution.

A Gabriel's horn is a type of geometric figure that has infinite surface area but finite volume. The name refers to the Christian tradition where the archangel Gabriel blows the horn to announce Judgment Day. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli in the 17th century.
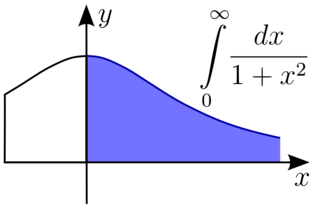
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.

In mathematics, Pappus's centroid theorem is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution.
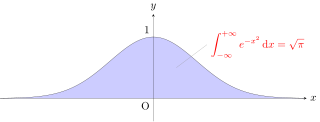
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is

In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
In mathematics, the stationary phase approximation is a basic principle of asymptotic analysis, applying to functions given by integration against a rapidly-varying complex exponential.
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an or with a . In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system.
In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in (the real-number plane) are called double integrals, and integrals of a function of three variables over a region in (real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, the Euclidean n-space of dimension n=3 that models physical space. More general three-dimensional spaces are called 3-manifolds.
In calculus, interchange of the order of integration is a methodology that transforms iterated integrals of functions into other, hopefully simpler, integrals by changing the order in which the integrations are performed. In some cases, the order of integration can be validly interchanged; in others it cannot.























