
The number e is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted . Alternatively, e can be called Napier's constant after John Napier. The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest.
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function.

L'Hôpital's rule or L'Hospital's rule, also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume De l'Hôpital. Although the rule is often attributed to De l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function, the radius of convergence is the shortest or minimum of all the respective distances calculated from the center of the disk of convergence to the respective singularities of the function.

In mathematics, the Lambert W function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the converse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function. The function is named after Johann Lambert, who considered a related problem in 1758. Building on Lambert's work, Leonhard Euler described the W function per se in 1783.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function.
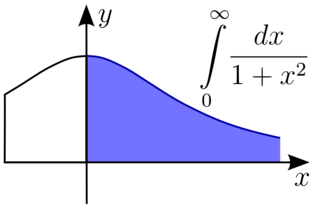
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In calculus, it is usually possible to compute the limit of the sum, difference, product, quotient or power of two functions by taking the corresponding combination of the separate limits of each respective function. For example,

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation and the left-exponent xb are common.
In mathematics, the exponential function can be characterized in many ways. This article presents some common characterizations, discusses why each makes sense, and proves that they are all equivalent.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form where and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative.
In discrete calculus the indefinite sum operator, denoted by or , is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus
Kaniadakis statistics is a generalization of Boltzmann–Gibbs statistical mechanics, based on a relativistic generalization of the classical Boltzmann–Gibbs–Shannon entropy. Introduced by the Greek Italian physicist Giorgio Kaniadakis in 2001, κ-statistical mechanics preserve the main features of ordinary statistical mechanics and have attracted the interest of many researchers in recent years. The κ-distribution is currently considered one of the most viable candidates for explaining complex physical, natural or artificial systems involving power-law tailed statistical distributions. Kaniadakis statistics have been adopted successfully in the description of a variety of systems in the fields of cosmology, astrophysics, condensed matter, quantum physics, seismology, genomics, economics, epidemiology, and many others.
























































































































