
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance.

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by or , is equal to the binomial coefficient
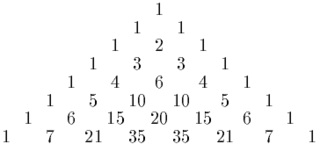
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a wide number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
In mathematics, a recurrence relation is an equation according to which the th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of ; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Generating functions are often expressed in closed form, by some expression involving operations on the formal series.

The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as and . They can be defined in several equivalent ways, one of which starts with trigonometric functions:
In mathematics, Bertrand's postulate states that, for each , there is a prime such that . First conjectured in 1845 by Joseph Bertrand, it was first proven by Chebyshev, and a shorter but also advanced proof was given by Ramanujan.
In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.
Multi-index notation is a mathematical notation that simplifies formulas used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices.
In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like for a nonnegative integer . Specifically, the binomial series is the MacLaurin series for the function , where and . Explicitly,
In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as or , is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over , a finite field with q elements; i.e. it is the number of points in the finite Grassmannian .
In mathematics the nth central binomial coefficient is the particular binomial coefficient
In mathematics, Pascal's rule is a combinatorial identity about binomial coefficients. It states that for positive natural numbers n and k, where is a binomial coefficient; one interpretation of the coefficient of the xk term in the expansion of (1 + x)n. There is no restriction on the relative sizes of n and k, since, if n < k the value of the binomial coefficient is zero and the identity remains valid.
In number theory, Lucas's theorem expresses the remainder of division of the binomial coefficient by a prime number p in terms of the base p expansions of the integers m and n.
In combinatorics, stars and bars is a graphical aid for deriving certain combinatorial theorems. It can be used to solve many simple counting problems, such as how many ways there are to put n indistinguishable balls into k distinguishable bins.
In mathematics, the Mittag-Leffler polynomials are the polynomials gn(x) or Mn(x) studied by Mittag-Leffler (1891).
In mathematics, Kummer's theorem is a formula for the exponent of the highest power of a prime number p that divides a given binomial coefficient. In other words, it gives the p-adic valuation of a binomial coefficient. The theorem is named after Ernst Kummer, who proved it in a paper,.











































































































