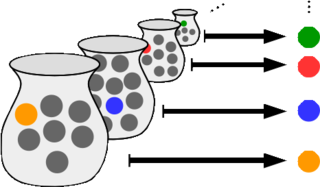
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces.

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equality. Any number is equal to itself (reflexive). If , then (symmetric). If and , then (transitive).

Naive Set Theory is a mathematics textbook by Paul Halmos providing an undergraduate introduction to set theory. Originally published by Van Nostrand in 1960, it was reprinted in the Springer-Verlag Undergraduate Texts in Mathematics series in 1974.

In mathematics, a set is a collection of different things; these things are called elements or members of the set and are typically mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets. A set may have a finite number of elements or be an infinite set. There is a unique set with no elements, called the empty set; a set with a single element is a singleton.
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation on some set , which satisfies the following for all and in :
- (reflexive).
- If and then (transitive).
- If and then (antisymmetric).
- or .
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology. For a list of terms specific to algebraic topology, see Glossary of algebraic topology.

In set theory, the union of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other. A nullary union refers to a union of zero sets and it is by definition equal to the empty set.
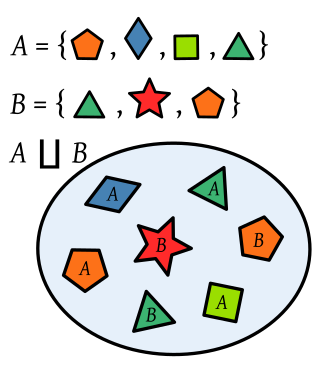
In mathematics, the disjoint union of the sets A and B is the set formed from the elements of A and B labelled (indexed) with the name of the set from which they come. So, an element belonging to both A and B appears twice in the disjoint union, with two different labels.

In mathematics, the symmetric difference of two sets, also known as the disjunctive union and set sum, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets and is .

In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset.
In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a topologically invariant way.
In mathematics, two sets are almost disjoint if their intersection is small in some sense; different definitions of "small" will result in different definitions of "almost disjoint".
In the mathematical field of measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. The theory of outer measures was first introduced by Constantin Carathéodory to provide an abstract basis for the theory of measurable sets and countably additive measures. Carathéodory's work on outer measures found many applications in measure-theoretic set theory, and was used in an essential way by Hausdorff to define a dimension-like metric invariant now called Hausdorff dimension. Outer measures are commonly used in the field of geometric measure theory.
In set theory and related branches of mathematics, a family can mean, depending upon the context, any of the following: set, indexed set, multiset, or class. A collection of subsets of a given set is called a family of subsets of , or a family of sets over More generally, a collection of any sets whatsoever is called a family of sets, set family, or a set system. Additionally, a family of sets may be defined as a function from a set , known as the index set, to , in which case the sets of the family are indexed by members of . In some contexts, a family of sets may be allowed to contain repeated copies of any given member, and in other contexts it may form a proper class.
In mathematics, particularly in combinatorics, given a family of sets, here called a collection C, a transversal (also called a cross-section) is a set containing exactly one element from each member of the collection. When the sets of the collection are mutually disjoint, each element of the transversal corresponds to exactly one member of C (the set it is a member of). If the original sets are not disjoint, there are two possibilities for the definition of a transversal:
In mathematics, a Grothendieck universe is a set U with the following properties:
- If x is an element of U and if y is an element of x, then y is also an element of U. (U is a transitive set.)
- If x and y are both elements of U, then is an element of U.
- If x is an element of U, then P(x), the power set of x, is also an element of U.
- If is a family of elements of U, and if I is an element of U, then the union is an element of U.

In the mathematical fields of set theory and extremal combinatorics, a sunflower or -system is a collection of sets in which all possible distinct pairs of sets share the same intersection. This common intersection is called the kernel of the sunflower.
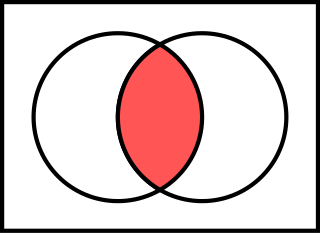
In set theory, the intersection of two sets and denoted by is the set containing all elements of that also belong to or equivalently, all elements of that also belong to
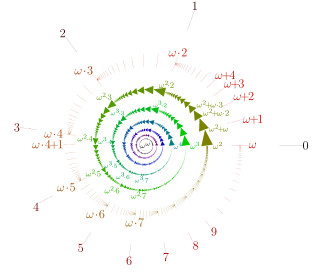
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.




















