In mathematics, a quadratic integral is an integral of the form
Contents
It can be evaluated by completing the square in the denominator.
In mathematics, a quadratic integral is an integral of the form
It can be evaluated by completing the square in the denominator.
Assume that the discriminant q = b2 − 4ac is positive. In that case, define u and A by
and
The quadratic integral can now be written as
The partial fraction decomposition
allows us to evaluate the integral:
The final result for the original integral, under the assumption that q > 0, is
In case the discriminant q = b2 − 4ac is negative, the second term in the denominator in
is positive. Then the integral becomes
In mathematics, Catalan's constantG, is defined by

In mathematics, the Lambert W function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the converse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form
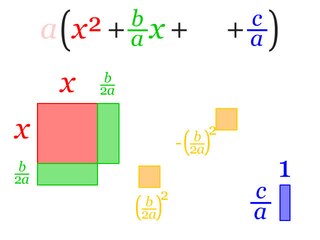
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. In calculus, trigonometric substitution is a technique for evaluating integrals. Moreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.
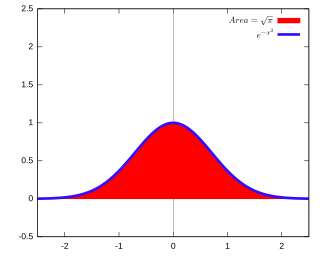
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Leibniz, states that for an integral of the form
In integral calculus, the Weierstrass substitution or tangent half-angle substitution is a method for evaluating integrals, which converts a rational function of trigonometric functions of into an ordinary rational function of by setting . No generality is lost by taking these to be rational functions of the sine and cosine. The general transformation formula is
Euler substitution is a method for evaluating integrals of the form