In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation,

In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.

The number e, also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithms. It is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series

The exponential function is a mathematical function denoted by or . Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation, but modern definitions allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics".

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space Cn. The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (analytic). Holomorphic functions are the central objects of study in complex analysis.

In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number x to the base b is the exponent to which b must be raised, to produce x. For example, since 1000 = 103, the logarithm base 10 of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x, or even without the explicit base, log x, when no confusion is possible, or when the base does not matter such as in big O notation.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

A logistic function or logistic curve is a common S-shaped curve with equation

In mathematics, exponentiation is an operation involving two numbers, the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; this pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.
In calculus, the power rule is used to differentiate functions of the form , whenever is a real number. Since differentiation is a linear operation on the space of differentiable functions, polynomials can also be differentiated using this rule. The power rule underlies the Taylor series as it relates a power series with a function's derivatives.

In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered its use, as well as standard logarithm. Historically, it was known as logarithmus decimalis or logarithmus decadis. It is indicated by log(x), log10 (x), or sometimes Log(x) with a capital L (however, this notation is ambiguous, since it can also mean the complex natural logarithmic multi-valued function). On calculators, it is printed as "log", but mathematicians usually mean natural logarithm (logarithm with base e ≈ 2.71828) rather than common logarithm when they write "log". To mitigate this ambiguity, the ISO 80000 specification recommends that log10 (x) should be written lg(x), and loge (x) should be ln(x).
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let where both f and g are differentiable and The quotient rule states that the derivative of h(x) is
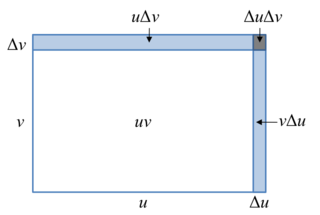
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as

In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form

In complex analysis, the argument principle relates the difference between the number of zeros and poles of a meromorphic function to a contour integral of the function's logarithmic derivative.
This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the logarithmic derivative of a function f,
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.










































