
In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.
In mathematics, a series is, roughly speaking, an addition of infinitely many terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures in combinatorics through generating functions. The mathematical properties of infinite series make them widely applicable in other quantitative disciplines such as physics, computer science, statistics and finance.

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of Göttingen in 1854, but not published in a journal until 1868. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration, or simulated using Monte Carlo integration.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if A convergent series that is not absolutely convergent is called conditionally convergent.
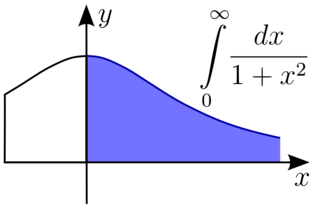
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In mathematics, the Henstock–Kurzweil integral or generalized Riemann integral or gauge integral – also known as the (narrow) Denjoy integral, Luzin integral or Perron integral, but not to be confused with the more general wide Denjoy integral – is one of a number of inequivalent definitions of the integral of a function. It is a generalization of the Riemann integral, and in some situations is more general than the Lebesgue integral. In particular, a function is Lebesgue integrable over a subset of if and only if the function and its absolute value are Henstock–Kurzweil integrable.

In mathematics, the integral test for convergence is a method used to test infinite series of monotonic terms for convergence. It was developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test.
In mathematics, an alternating series is an infinite series of terms that alternate between positive and negative signs. In capital-sigma notation this is expressed or with an > 0 for all n.
In mathematical analysis, Cesàro summation assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as n tends to infinity, of the sequence of arithmetic means of the first n partial sums of the series.
In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin-Louis Cauchy.
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:
In mathematics, the root test is a criterion for the convergence of an infinite series. It depends on the quantity
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence defines a series S that is denoted
In mathematics, weak convergence in a Hilbert space is the convergence of a sequence of points in the weak topology.
In mathematics, the Cauchy condensation test, named after Augustin-Louis Cauchy, is a standard convergence test for infinite series. For a non-increasing sequence of non-negative real numbers, the series converges if and only if the "condensed" series converges. Moreover, if they converge, the sum of the condensed series is no more than twice as large as the sum of the original.
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series .
In mathematics, Abel's test is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Henrik Abel, who proved it in 1826. There are two slightly different versions of Abel's test – one is used with series of real numbers, and the other is used with power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.






































