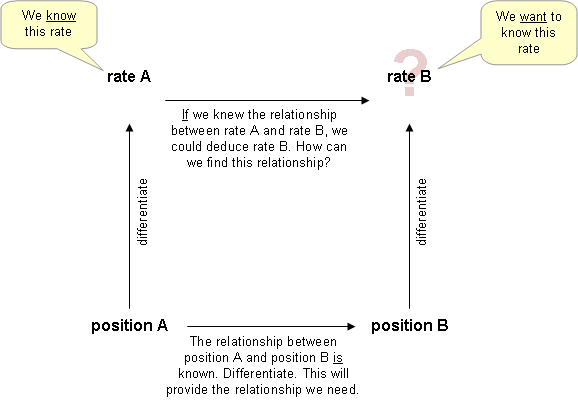
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation,

In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.
In mathematics, an implicit equation is a relation of the form where R is a function of several variables. For example, the implicit equation of the unit circle is

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero, and an exact form is a differential form, α, that is the exterior derivative of another differential form β. Thus, an exact form is in the image of d, and a closed form is in the kernel of d.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.
In mathematics, the total derivative of a function f at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when f is a function of several variables, because when f is a function of a single variable, the total derivative is the same as the ordinary derivative of the function.
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers , or a subset of that contains an interval of positive length. Most real functions that are considered and studied are differentiable in some interval. The most widely considered such functions are the real functions, which are the real-valued functions of a real variable, that is, the functions of a real variable whose codomain is the set of real numbers.
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as .
In calculus, a parametric derivative is a derivative of a dependent variable with respect to another dependent variable that is taken when both variables depend on an independent third variable, usually thought of as "time".
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with functions of other variables. The intent is that when expressed in new variables, the problem may become simpler, or equivalent to a better understood problem.
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Leibniz, states that for an integral of the form

In mathematics, a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in are called double integrals, and integrals of a function of three variables over a region in are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

In calculus, the second derivative, or the second order derivative, of a function f is the derivative of the derivative of f. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of the object is changing with respect to time. In Leibniz notation:

In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis. Under reasonably generic assumptions about the dynamical system, a small-amplitude limit cycle branches from the fixed point.
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. For example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angle.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
In calculus, the differential represents the principal part of the change in a function y = f(x) with respect to changes in the independent variable. The differential dy is defined by