Graph of a function

For graph-theoretic representation of a function, see Functional graph.

Graph of the function ${\displaystyle f(x)={\frac {x^{3}+3x^{2}-6x-8}{4}}.}$

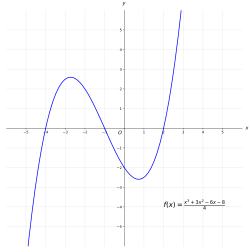
In mathematics, the graph of a function${\displaystyle f}$ is the set of ordered pairs ${\displaystyle (x,y)}$, where ${\displaystyle f(x)=y.}$ In the common case where ${\displaystyle x}$ and ${\displaystyle f(x)}$ are real numbers, these pairs are Cartesian coordinates of points in a plane and often form a curve. The graphical representation of the graph of a function is also known as a plot .

In the case of functions of two variables – that is, functions whose domain consists of pairs ${\displaystyle (x,y)}$ –, the graph usually refers to the set of ordered triples ${\displaystyle (x,y,z)}$ where ${\displaystyle f(x,y)=z}$. This is a subset of three-dimensional space; for a continuous real-valued function of two real variables, its graph forms a surface, which can be visualized as a surface plot .

In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see Plot (graphics) for details.

A graph of a function is a special case of a relation. In the modern foundations of mathematics, and, typically, in set theory, a function is actually equal to its graph. ^[1] However, it is often useful to see functions as mappings, ^[2] which consist not only of the relation between input and output, but also which set is the domain, and which set is the codomain. For example, to say that a function is onto (surjective) or not the codomain should be taken into account. The graph of a function on its own does not determine the codomain. It is common ^[3] to use both terms function and graph of a function since even if considered the same object, they indicate viewing it from a different perspective.

Graph of the function ${\displaystyle f(x)=x^{4}-4^{x}}$ over the interval [−2,+3]. Also shown are the two real roots and the local minimum that are in the interval.

Definition

Given a function ${\displaystyle f:X\to Y}$ from a set X (the domain) to a set Y (the codomain), the graph of the function is the set ^[4]

$${\displaystyle G(f)=\{(x,f(x)):x\in X\},}$$

which is a subset of the Cartesian product ${\displaystyle X\times Y}$. In the definition of a function in terms of set theory, it is common to identify a function with its graph, although, formally, a function is formed by the triple consisting of its domain, its codomain and its graph.

Examples

Functions of one variable

Graph of the function ${\displaystyle f(x,y)=\sin \left(x^{2}\right)\cdot \cos \left(y^{2}\right).}$

The graph of the function ${\displaystyle f:\{1,2,3\}\to \{a,b,c,d\}}$ defined by

$${\displaystyle f(x)={\begin{cases}a,&{\text{if }}x=1,\\d,&{\text{if }}x=2,\\c,&{\text{if }}x=3,\end{cases}}}$$

is the subset of the set ${\displaystyle \{1,2,3\}\times \{a,b,c,d\}}$

$${\displaystyle G(f)=\{(1,a),(2,d),(3,c)\}.}$$

From the graph, the domain ${\displaystyle \{1,2,3\}}$ is recovered as the set of first component of each pair in the graph ${\displaystyle \{1,2,3\}=\{x:\ \exists y,{\text{ such that }}(x,y)\in G(f)\}}$. Similarly, the range can be recovered as ${\displaystyle \{a,c,d\}=\{y:\exists x,{\text{ such that }}(x,y)\in G(f)\}}$. The codomain ${\displaystyle \{a,b,c,d\}}$, however, cannot be determined from the graph alone.

The graph of the cubic polynomial on the real line

$${\displaystyle f(x)=x^{3}-9x}$$

is

$${\displaystyle \{(x,x^{3}-9x):x{\text{ is a real number}}\}.}$$

If this set is plotted on a Cartesian plane, the result is a curve (see figure).

Functions of two variables

Plot of the graph of ${\displaystyle f(x,y)=-\left(\cos \left(x^{2}\right)+\cos \left(y^{2}\right)\right)^{2},}$ also showing its gradient projected on the bottom plane.

The graph of the trigonometric function

$${\displaystyle f(x,y)=\sin(x^{2})\cos(y^{2})}$$

is

$${\displaystyle \{(x,y,\sin(x^{2})\cos(y^{2})):x{\text{ and }}y{\text{ are real numbers}}\}.}$$

If this set is plotted on a three dimensional Cartesian coordinate system, the result is a surface (see figure).

Oftentimes it is helpful to show with the graph, the gradient of the function and several level curves. The level curves can be mapped on the function surface or can be projected on the bottom plane. The second figure shows such a drawing of the graph of the function:

$${\displaystyle f(x,y)=-(\cos(x^{2})+\cos(y^{2}))^{2}.}$$

See also

• Asymptote
• Chart
• Plot
• Concave function
• Convex function
• Contour plot
• Critical point
• Derivative
• Epigraph
• Normal to a graph
• Slope
• Stationary point
• Tetraview
• Vertical translation
• y-intercept

References

1. Charles C Pinter (2014) [1971]. A Book of Set Theory. Dover Publications. p. 49. ISBN   978-0-486-79549-2.
2. T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. p. 35.
3. P. R. Halmos (1982). A Hilbert Space Problem Book . Springer-Verlag. p.  31. ISBN   0-387-90685-1.
4. D. S. Bridges (1991). Foundations of Real and Abstract Analysis. Springer. p.  285. ISBN   0-387-98239-6.

Further reading

• Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces . River Edge, N.J. London: World Scientific Publishing. ISBN   978-981-4488-15-0. MR   1921556. OCLC   285163112 – via Internet Archive.

External links

• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.