
Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
In mathematics, more specifically in ring theory, a Euclidean domain is an integral domain that can be endowed with a Euclidean function which allows a suitable generalization of the Euclidean division of integers. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them. Also every ideal in a Euclidean domain is principal, which implies a suitable generalization of the fundamental theorem of arithmetic: every Euclidean domain is a unique factorization domain.

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.

A random variable is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function in which

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. Informally, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
In mathematics, more specifically in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on algebraic varieties or manifolds, or of algebraic number fields examined at a particular place, or prime. Local algebra is the branch of commutative algebra that studies commutative local rings and their modules.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.

Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.

In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some algebraic structures, such as ordered or normed groups, and fields. The property, as typically construed, states that given two positive numbers and , there is an integer such that . It also means that the set of natural numbers is not bounded above. Roughly speaking, it is the property of having no infinitely large or infinitely small elements. It was Otto Stolz who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes’ On the Sphere and Cylinder.
In algebra, a valuation is a function on a field that provides a measure of the size or multiplicity of elements of the field. It generalizes to commutative algebra the notion of size inherent in consideration of the degree of a pole or multiplicity of a zero in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic or analytic varieties in algebraic geometry. A field with a valuation on it is called a valued field.
In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols can denote numbers (constants), variables, operations, and functions. Other symbols include punctuation signs and brackets.
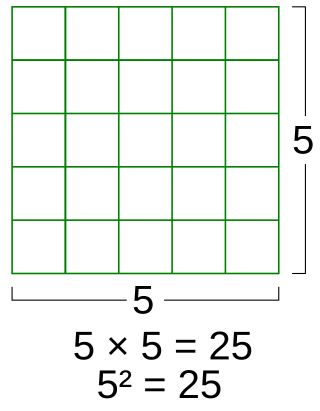
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
In abstract algebra, a discrete valuation ring (DVR) is a principal ideal domain (PID) with exactly one non-zero maximal ideal.

In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator p and a non-zero denominator q. For example, is a rational number, as is every integer. The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface Q, or blackboard bold

In mathematics, a real-valued function is a function whose values are real numbers. In other words, it is a function that assigns a real number to each member of its domain.
In mathematics, an algebraic number field is an extension field of the field of rational numbers such that the field extension has finite degree . Thus is a field that contains and has finite dimension when considered as a vector space over .










