
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to .
In mathematics and computer programming, exponentiating by squaring is a general method for fast computation of large positive integer powers of a number, or more generally of an element of a semigroup, like a polynomial or a square matrix. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. These can be of quite general use, for example in modular arithmetic or powering of matrices. For semigroups for which additive notation is commonly used, like elliptic curves used in cryptography, this method is also referred to as double-and-add.

In mathematics and computer science, the floor function is the function that takes as input a real number x, and gives as output the greatest integer less than or equal to x, denoted ⌊x⌋ or floor(x). Similarly, the ceiling function maps x to the smallest integer greater than or equal to x, denoted ⌈x⌉ or ceil(x).
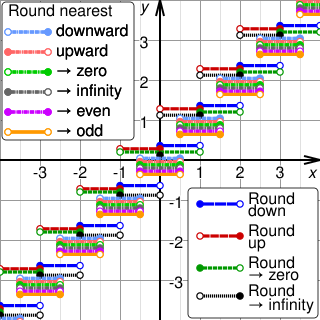
Rounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $23.4476 with $23.45, the fraction 312/937 with 1/3, or the expression √2 with 1.414.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operations and directly supported by the processor. Most bitwise operations are presented as two-operand instructions where the result replaces one of the input operands.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).

In number theory, the Mertens function is defined for all positive integers n as
The fractional part or decimal part of a non‐negative real number is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than x, called floor of x or . Then, the fractional part can be formulated as a difference:
In mathematics, a pairing function is a process to uniquely encode two natural numbers into a single natural number.
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another.
Methods of computing square roots are algorithms for approximating the non-negative square root of a positive real number . Since all square roots of natural numbers, other than of perfect squares, are irrational, square roots can usually only be computed to some finite precision: these methods typically construct a series of increasingly accurate approximations.
In number theory, the law of quadratic reciprocity, like the Pythagorean theorem, has lent itself to an unusually large number of proofs. Several hundred proofs of the law of quadratic reciprocity have been published.
Shanks's square forms factorization is a method for integer factorization devised by Daniel Shanks as an improvement on Fermat's factorization method.
The digital root of a natural number in a given radix is the value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached. For example, in base 10, the digital root of the number 12345 is 6 because the sum of the digits in the number is 1 + 2 + 3 + 4 + 5 = 15, then the addition process is repeated again for the resulting number 15, so that the sum of 1 + 5 equals 6, which is the digital root of that number. In base 10, this is equivalent to taking the remainder upon division by 9, which allows it to be used as a divisibility rule.
In mathematics, an infinite periodic continued fraction is a continued fraction that can be placed in the form
In computer science, multiply-with-carry (MWC) is a method invented by George Marsaglia for generating sequences of random integers based on an initial set from two to many thousands of randomly chosen seed values. The main advantages of the MWC method are that it invokes simple computer integer arithmetic and leads to very fast generation of sequences of random numbers with immense periods, ranging from around to .

In probability theory and statistics, the Conway–Maxwell–Poisson distribution is a discrete probability distribution named after Richard W. Conway, William L. Maxwell, and Siméon Denis Poisson that generalizes the Poisson distribution by adding a parameter to model overdispersion and underdispersion. It is a member of the exponential family, has the Poisson distribution and geometric distribution as special cases and the Bernoulli distribution as a limiting case.
































































