Boolean function

Last updated December 23, 2024

In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually {true, false}, {0,1} or {-1,1}).^[1]^[2] Alternative names are switching function, used especially in older computer science literature,^[3]^[4] and truth function (or logical function), used in logic. Boolean functions are the subject of Boolean algebra and switching theory.^[5]

A Boolean function takes the form $f:\{0,1\}^{k}\to \{0,1\}$ , where $\{0,1\}$ is known as the Boolean domain and $k$ is a non-negative integer called the arity of the function. In the case where $k=0$ , the function is a constant element of $\{0,1\}$ . A Boolean function with multiple outputs, $f:\{0,1\}^{k}\to \{0,1\}^{m}$ with $m>1$ is a vectorial or vector-valued Boolean function (an S-box in symmetric cryptography).^[6]

There are $2^{2^{k}}$ different Boolean functions with $k$ arguments; equal to the number of different truth tables with $2^{k}$ entries.

Every $k$ -ary Boolean function can be expressed as a propositional formula in $k$ variables $x_{1},...,x_{k}$ , and two propositional formulas are logically equivalent if and only if they express the same Boolean function.

Examples

The rudimentary symmetric Boolean functions (logical connectives or logic gates) are:

NOT, negation or complement - which receives one input and returns true when that input is false ("not")
AND or conjunction - true when all inputs are true ("both")
OR or disjunction - true when any input is true ("either")
XOR or exclusive disjunction - true when one of its inputs is true and the other is false ("not equal")
NAND or Sheffer stroke - true when it is not the case that all inputs are true ("not both")
NOR or logical nor - true when none of the inputs are true ("neither")
XNOR or logical equality - true when both inputs are the same ("equal")

An example of a more complicated function is the majority function (of an odd number of inputs).

Representation

A Boolean function may be specified in a variety of ways:

Truth table: explicitly listing its value for all possible values of the arguments
- Marquand diagram: truth table values arranged in a two-dimensional grid (used in a Karnaugh map)
- Binary decision diagram, listing the truth table values at the bottom of a binary tree
- Venn diagram, depicting the truth table values as a colouring of regions of the plane

Algebraically, as a propositional formula using rudimentary Boolean functions:

Negation normal form, an arbitrary mix of AND and ORs of the arguments and their complements
Disjunctive normal form, as an OR of ANDs of the arguments and their complements
Conjunctive normal form, as an AND of ORs of the arguments and their complements
Canonical normal form, a standardized formula which uniquely identifies the function:
- Algebraic normal form or Zhegalkin polynomial, as a XOR of ANDs of the arguments (no complements allowed)
- Full (canonical) disjunctive normal form, an OR of ANDs each containing every argument or complement (minterms)
- Full (canonical) conjunctive normal form, an AND of ORs each containing every argument or complement (maxterms)
- Blake canonical form, the OR of all the prime implicants of the function

Boolean formulas can also be displayed as a graph:

Propositional directed acyclic graph
- Digital circuit diagram of logic gates, a Boolean circuit
- And-inverter graph, using only AND and NOT

In order to optimize electronic circuits, Boolean formulas can be minimized using the Quine–McCluskey algorithm or Karnaugh map.

Analysis

Properties

A Boolean function can have a variety of properties:^[7]

Constant: Is always true or always false regardless of its arguments.
Monotone: for every combination of argument values, changing an argument from false to true can only cause the output to switch from false to true and not from true to false. A function is said to be unate in a certain variable if it is monotone with respect to changes in that variable.
Linear: for each variable, flipping the value of the variable either always makes a difference in the truth value or never makes a difference (a parity function).
Symmetric: the value does not depend on the order of its arguments.
Read-once: Can be expressed with conjunction, disjunction, and negation with a single instance of each variable.
Balanced: if its truth table contains an equal number of zeros and ones. The Hamming weight of the function is the number of ones in the truth table.
Bent: its derivatives are all balanced (the autocorrelation spectrum is zero)
Correlation immune to mth order: if the output is uncorrelated with all (linear) combinations of at most m arguments
Evasive: if evaluation of the function always requires the value of all arguments
A Boolean function is a Sheffer function if it can be used to create (by composition) any arbitrary Boolean function (see functional completeness)
The algebraic degree of a function is the order of the highest order monomial in its algebraic normal form

Circuit complexity attempts to classify Boolean functions with respect to the size or depth of circuits that can compute them.

Derived functions

A Boolean function may be decomposed using Boole's expansion theorem in positive and negative Shannoncofactors (Shannon expansion), which are the (k-1)-ary functions resulting from fixing one of the arguments (to zero or one). The general (k-ary) functions obtained by imposing a linear constraint on a set of inputs (a linear subspace) are known as subfunctions.^[8]

The Boolean derivative of the function to one of the arguments is a (k-1)-ary function that is true when the output of the function is sensitive to the chosen input variable; it is the XOR of the two corresponding cofactors. A derivative and a cofactor are used in a Reed–Muller expansion. The concept can be generalized as a k-ary derivative in the direction dx, obtained as the difference (XOR) of the function at x and x + dx.^[8]

The Möbius transform (or Boole-Möbius transform) of a Boolean function is the set of coefficients of its polynomial (algebraic normal form), as a function of the monomial exponent vectors. It is a self-inverse transform. It can be calculated efficiently using a butterfly algorithm ("Fast Möbius Transform"), analogous to the Fast Fourier Transform.^[9]Coincident Boolean functions are equal to their Möbius transform, i.e. their truth table (minterm) values equal their algebraic (monomial) coefficients.^[10] There are 2^2^(k−1) coincident functions of k arguments.^[11]

Cryptographic analysis

The Walsh transform of a Boolean function is a k-ary integer-valued function giving the coefficients of a decomposition into linear functions (Walsh functions), analogous to the decomposition of real-valued functions into harmonics by the Fourier transform. Its square is the power spectrum or Walsh spectrum. The Walsh coefficient of a single bit vector is a measure for the correlation of that bit with the output of the Boolean function. The maximum (in absolute value) Walsh coefficient is known as the linearity of the function.^[8] The highest number of bits (order) for which all Walsh coefficients are 0 (i.e. the subfunctions are balanced) is known as resiliency, and the function is said to be correlation immune to that order.^[8] The Walsh coefficients play a key role in linear cryptanalysis.

The autocorrelation of a Boolean function is a k-ary integer-valued function giving the correlation between a certain set of changes in the inputs and the function output. For a given bit vector it is related to the Hamming weight of the derivative in that direction. The maximal autocorrelation coefficient (in absolute value) is known as the absolute indicator.^[7]^[8] If all autocorrelation coefficients are 0 (i.e. the derivatives are balanced) for a certain number of bits then the function is said to satisfy the propagation criterion to that order; if they are all zero then the function is a bent function.^[12] The autocorrelation coefficients play a key role in differential cryptanalysis.

The Walsh coefficients of a Boolean function and its autocorrelation coefficients are related by the equivalent of the Wiener–Khinchin theorem, which states that the autocorrelation and the power spectrum are a Walsh transform pair.^[8]

Linear approximation table

These concepts can be extended naturally to vectorial Boolean functions by considering their output bits (coordinates) individually, or more thoroughly, by looking at the set of all linear functions of output bits, known as its components.^[6] The set of Walsh transforms of the components is known as a Linear Approximation Table (LAT)^[13]^[14] or correlation matrix;^[15]^[16] it describes the correlation between different linear combinations of input and output bits. The set of autocorrelation coefficients of the components is the autocorrelation table,^[14] related by a Walsh transform of the components^[17] to the more widely used Difference Distribution Table (DDT)^[13]^[14] which lists the correlations between differences in input and output bits (see also: S-box).

Real polynomial form

On the unit hypercube

Any Boolean function $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ can be uniquely extended (interpolated) to the real domain by a multilinear polynomial in $\mathbb {R} ^{n}$ , constructed by summing the truth table values multiplied by indicator polynomials: $f^{*}(x)=\sum _{a\in {\{0,1\}}^{n}}f(a)\prod _{i:a_{i}=1}x_{i}\prod _{i:a_{i}=0}(1-x_{i})$ For example, the extension of the binary XOR function $x\oplus y$ is $0(1-x)(1-y)+1x(1-y)+1(1-x)y+0xy$ which equals $x+y-2xy$ Some other examples are negation ( $1-x$ ), AND ( $xy$ ) and OR ( $x+y-xy$ ). When all operands are independent (share no variables) a function's polynomial form can be found by repeatedly applying the polynomials of the operators in a Boolean formula. When the coefficients are calculated modulo 2 one obtains the algebraic normal form (Zhegalkin polynomial).

Direct expressions for the coefficients of the polynomial can be derived by taking an appropriate derivative: ${\begin{array}{lcl}f^{*}(00)&=&(f^{*})(00)&=&f(00)\\f^{*}(01)&=&(\partial _{1}f^{*})(00)&=&-f(00)+f(01)\\f^{*}(10)&=&(\partial _{2}f^{*})(00)&=&-f(00)+f(10)\\f^{*}(11)&=&(\partial _{1}\partial _{2}f^{*})(00)&=&f(00)-f(01)-f(10)+f(11)\\\end{array}}$ this generalizes as the Möbius inversion of the partially ordered set of bit vectors: $f^{*}(m)=\sum _{a\subseteq m}(-1)^{|a|+|m|}f(a)$ where $|a|$ denotes the weight of the bit vector $a$ . Taken modulo 2, this is the Boolean Möbius transform, giving the algebraic normal form coefficients: ${\hat {f}}(m)=\bigoplus _{a\subseteq m}f(a)$ In both cases, the sum is taken over all bit-vectors a covered by m, i.e. the "one" bits of a form a subset of the one bits of m.

When the domain is restricted to the n-dimensional hypercube $[0,1]^{n}$ , the polynomial $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ gives the probability of a positive outcome when the Boolean function f is applied to n independent random (Bernoulli) variables, with individual probabilities x. A special case of this fact is the piling-up lemma for parity functions. The polynomial form of a Boolean function can also be used as its natural extension to fuzzy logic.

On the symmetric hypercube

Often, the Boolean domain is taken as $\{-1,1\}$ , with false ("0") mapping to 1 and true ("1") to -1 (see Analysis of Boolean functions). The polynomial corresponding to $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ is then given by: $g^{*}(x)=\sum _{a\in {\{-1,1\}}^{n}}g(a)\prod _{i:a_{i}=-1}{\frac {1-x_{i}}{2}}\prod _{i:a_{i}=1}{\frac {1+x_{i}}{2}}$ Using the symmetric Boolean domain simplifies certain aspects of the analysis, since negation corresponds to multiplying by -1 and linear functions are monomials (XOR is multiplication). This polynomial form thus corresponds to the Walsh transform (in this context also known as Fourier transform) of the function (see above). The polynomial also has the same statistical interpretation as the one in the standard Boolean domain, except that it now deals with the expected values $E(X)=P(X=1)-P(X=-1)\in [-1,1]$ (see piling-up lemma for an example).

Applications

Boolean functions play a basic role in questions of complexity theory as well as the design of processors for digital computers, where they are implemented in electronic circuits using logic gates.

The properties of Boolean functions are critical in cryptography, particularly in the design of symmetric key algorithms (see substitution box).

In cooperative game theory, monotone Boolean functions are called simple games (voting games); this notion is applied to solve problems in social choice theory.

Related Research Articles

Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.

In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

In mathematics, the term linear is used in two distinct senses for two different properties:

In mathematics, an algebra over a field is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear".

In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form $where a 0 (x), ..., a n (x) and b (x) are arbitrary differentiable functions that do not need to be linear, and y', ..., y (n) are the successive derivatives of an unknown function y of the variable x .$

A maximum length sequence (MLS) is a type of pseudorandom binary sequence.

Reed–Muller codes are error-correcting codes that are used in wireless communications applications, particularly in deep-space communication. Moreover, the proposed 5G standard relies on the closely related polar codes for error correction in the control channel. Due to their favorable theoretical and mathematical properties, Reed–Muller codes have also been extensively studied in theoretical computer science.

In mathematics, the correlation immunity of a Boolean function is a measure of the degree to which its outputs are uncorrelated with some subset of its inputs. Specifically, a Boolean function is said to be correlation-immune of order m if every subset of m or fewer variables in $is statistically independent of the value of .$

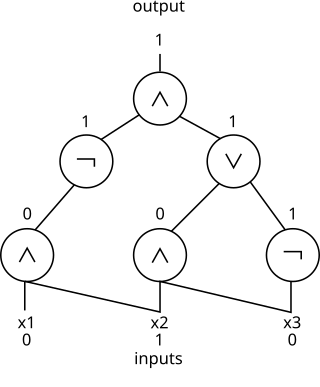
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the circuit complexity of a recursive language that is decided by a uniform family of circuits $.$

Zhegalkinpolynomials, also known as algebraic normal form, are a representation of functions in Boolean algebra. Introduced by the Russian mathematician Ivan Ivanovich Zhegalkin in 1927, they are the polynomial ring over the integers modulo 2. The resulting degeneracies of modular arithmetic result in Zhegalkin polynomials being simpler than ordinary polynomials, requiring neither coefficients nor exponents. Coefficients are redundant because 1 is the only nonzero coefficient. Exponents are redundant because in arithmetic mod 2, x² = x. Hence a polynomial such as 3x²y⁵z is congruent to, and can therefore be rewritten as, xyz.

In algebra, a multilinear polynomial is a multivariate polynomial that is linear in each of its variables separately, but not necessarily simultaneously. It is a polynomial in which no variable occurs to a power of $or higher; that is, each monomial is a constant times a product of distinct variables. For example is a multilinear polynomial of degree whereas is not. The degree of a multilinear polynomial is the maximum number of distinct variables occurring in any monomial.$

In mathematics, a symmetric Boolean function is a Boolean function whose value does not depend on the order of its input bits, i.e., it depends only on the number of ones in the input. For this reason they are also known as Boolean counting functions.

In Boolean algebra, a parity function is a Boolean function whose value is one if and only if the input vector has an odd number of ones. The parity function of two inputs is also known as the XOR function.

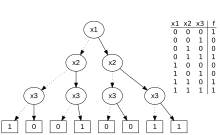
In computational complexity theory, the decision tree model is the model of computation in which an algorithm can be considered to be a decision tree, i.e. a sequence of queries or tests that are done adaptively, so the outcome of previous tests can influence the tests performed next.

In the mathematical field of combinatorics, a bent function is a Boolean function that is maximally non-linear; it is as different as possible from the set of all linear and affine functions when measured by Hamming distance between truth tables. Concretely, this means the maximum correlation between the output of the function and a linear function is minimal. In addition, the derivatives of a bent function are balanced Boolean functions, so for any change in the input variables there is a 50 percent chance that the output value will change.

A locally decodable code (LDC) is an error-correcting code that allows a single bit of the original message to be decoded with high probability by only examining a small number of bits of a possibly corrupted codeword. This property could be useful, say, in a context where information is being transmitted over a noisy channel, and only a small subset of the data is required at a particular time and there is no need to decode the entire message at once. Locally decodable codes are not a subset of locally testable codes, though there is some overlap between the two.

In cryptography, SWIFFT is a collection of provably secure hash functions. It is based on the concept of the fast Fourier transform (FFT). SWIFFT is not the first hash function based on the FFT, but it sets itself apart by providing a mathematical proof of its security. It also uses the LLL basis reduction algorithm. It can be shown that finding collisions in SWIFFT is at least as difficult as finding short vectors in cyclic/ideal lattices in the worst case. By giving a security reduction to the worst-case scenario of a difficult mathematical problem, SWIFFT gives a much stronger security guarantee than most other cryptographic hash functions.

In theoretical computer science, multiparty communication complexity is the study of communication complexity in the setting where there are more than 2 players.

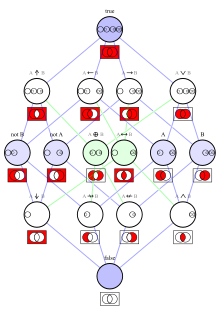
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as $\land$ , disjunction (or) denoted as $\lor$ , and negation (not) denoted as $\neg$ . Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations in the same way that elementary algebra describes numerical operations.

References

↑ "Boolean function - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-05-03.
↑ Weisstein, Eric W. "Boolean Function". mathworld.wolfram.com. Retrieved 2021-05-03.
↑ "switching function". TheFreeDictionary.com. Retrieved 2021-05-03.
↑ Davies, D. W. (December 1957). "Switching Functions of Three Variables". IRE Transactions on Electronic Computers. EC-6 (4): 265–275. doi:10.1109/TEC.1957.5222038. ISSN 0367-9950.
↑ McCluskey, Edward J. (2003-01-01), "Switching theory", Encyclopedia of Computer Science, GBR: John Wiley and Sons Ltd., pp. 1727–1731, ISBN 978-0-470-86412-8 , retrieved 2021-05-03
1 2 Carlet, Claude. "Vectorial Boolean Functions for Cryptography" (PDF). University of Paris. Archived (PDF) from the original on 2016-01-17.
1 2 "Boolean functions — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-01.
1 2 3 4 5 6 Tarannikov, Yuriy; Korolev, Peter; Botev, Anton (2001). "Autocorrelation Coefficients and Correlation Immunity of Boolean Functions". In Boyd, Colin (ed.). Advances in Cryptology — ASIACRYPT 2001. Lecture Notes in Computer Science. Vol. 2248. Berlin, Heidelberg: Springer. pp. 460–479. doi: 10.1007/3-540-45682-1_27 . ISBN 978-3-540-45682-7.
↑ Carlet, Claude (2010), "Boolean Functions for Cryptography and Error-Correcting Codes" (PDF), Boolean Models and Methods in Mathematics, Computer Science, and Engineering, Encyclopedia of Mathematics and its Applications, Cambridge: Cambridge University Press, pp. 257–397, ISBN 978-0-521-84752-0 , retrieved 2021-05-17
↑ Pieprzyk, Josef; Wang, Huaxiong; Zhang, Xian-Mo (2011-05-01). "Mobius transforms, coincident Boolean functions and non-coincidence property of Boolean functions". International Journal of Computer Mathematics. 88 (7): 1398–1416. doi:10.1080/00207160.2010.509428. ISSN 0020-7160. S2CID 9580510.
↑ Nitaj, Abderrahmane; Susilo, Willy; Tonien, Joseph (2017-10-01). "Dirichlet product for boolean functions". Journal of Applied Mathematics and Computing. 55 (1): 293–312. doi:10.1007/s12190-016-1037-4. ISSN 1865-2085. S2CID 16760125.
↑ Canteaut, Anne; Carlet, Claude; Charpin, Pascale; Fontaine, Caroline (2000-05-14). "Propagation characteristics and correlation-immunity of highly nonlinear boolean functions". Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques. EUROCRYPT'00. Bruges, Belgium: Springer-Verlag: 507–522. ISBN 978-3-540-67517-4.
1 2 Heys, Howard M. "A Tutorial on Linear and Differential Cryptanalysis" (PDF). Archived (PDF) from the original on 2017-05-17.
1 2 3 "S-Boxes and Their Algebraic Representations — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-04.
↑ Daemen, Joan; Govaerts, René; Vandewalle, Joos (1994). "Correlation matrices". In Preneel, Bart (ed.). Fast Software Encryption: Second International Workshop. Leuven, Belgium, 14-16 December 1994, Proceedings. Lecture Notes in Computer Science. Vol. 1008. Springer. pp. 275–285. doi: 10.1007/3-540-60590-8_21 .
↑ Daemen, Joan (10 June 1998). "Chapter 5: Propagation and Correlation - Annex to AES Proposal Rijndael" (PDF). NIST. Archived (PDF) from the original on 2018-07-23.
↑ Nyberg, Kaisa (December 1, 2019). "The Extended Autocorrelation and Boomerang Tables and Links Between Nonlinearity Properties of Vectorial Boolean Functions" (PDF). Archived (PDF) from the original on 2020-11-02.

v t e Function
History List of specific functions
Types by domain and codomain	$X \to 𝔹$ $𝔹 \to X$ $𝔹ⁿ \to X$ $X \to ℤ$ $ℤ \to X$ $X \to ℝ$ $ℝ \to X$ $ℝⁿ \to X$ $X \to ℂ$ $ℂ \to X$ $ℂⁿ \to X$
Classes/properties	Constant Identity Linear Polynomial Rational Algebraic Analytic Smooth Continuous Measurable Injective Surjective Bijective
Constructions	Restriction Composition λ Inverse
Generalizations	Relation (Binary relation) Set-valued Multivalued Partial Implicit Space Higher-order Morphism Functor
Category