In mathematics, a binary function is a function that takes two inputs.
The relational model (RM) for database management is an approach to managing data using a structure and language consistent with first-order predicate logic, first described in 1969 by English computer scientist Edgar F. Codd, where all data is represented in terms of tuples, grouped into relations. A database organized in terms of the relational model is a relational database.
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.

Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ.

In mathematics, the symmetric difference of two sets, also known as the disjunctive union, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets and is .

Mathematical morphology (MM) is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on graphs, surface meshes, solids, and many other spatial structures.
In logic, a truth function is a function that accepts truth values as input and produces a unique truth value as output. In other words: The input and output of a truth function are all truth values; a truth function will always output exactly one truth value; and inputting the same truth value(s) will always output the same truth value. The typical example is in propositional logic, wherein a compound statement is constructed using individual statements connected by logical connectives; if the truth value of the compound statement is entirely determined by the truth value(s) of the constituent statement(s), the compound statement is called a truth function, and any logical connectives used are said to be truth functional.

In mathematics, a Boolean function is a function whose arguments, as well as the function itself, assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
System F, also known as the (Girard–Reynolds) polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types. System F thus formalizes the notion of parametric polymorphism in programming languages, and forms a theoretical basis for languages such as Haskell and ML. System F was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds (1974).
In Boolean algebra, the algebraic normal form (ANF), ring sum normal form, Zhegalkin normal form, or Reed–Muller expansion is a way of writing logical formulas in one of three subforms:
In mathematics, fuzzy measure theory considers generalized measures in which the additive property is replaced by the weaker property of monotonicity. The central concept of fuzzy measure theory is the fuzzy measure which was introduced by Choquet in 1953 and independently defined by Sugeno in 1974 in the context of fuzzy integrals. There exists a number of different classes of fuzzy measures including plausibility/belief measures; possibility/necessity measures; and probability measures which are a subset of classical measures.
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients.
In mathematics, the correlation immunity of a Boolean function is a measure of the degree to which its outputs are uncorrelated with some subset of its inputs. Specifically, a Boolean function is said to be correlation-immune of order m if every subset of m or fewer variables in is statistically independent of the value of .
Zhegalkinpolynomials are a representation of functions in Boolean algebra. Introduced by the Russian mathematician Ivan Ivanovich Zhegalkin in 1927, they are the polynomial ring over the integers modulo 2. The resulting degeneracies of modular arithmetic result in Zhegalkin polynomials being simpler than ordinary polynomials, requiring neither coefficients nor exponents. Coefficients are redundant because 1 is the only nonzero coefficient. Exponents are redundant because in arithmetic mod 2, x2 = x. Hence a polynomial such as 3x2y5z is congruent to, and can therefore be rewritten as, xyz.
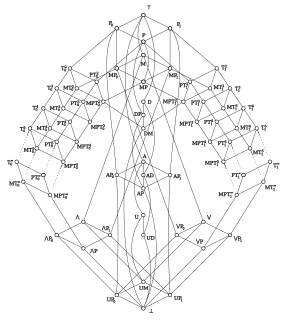
In logic and universal algebra, Post's lattice denotes the lattice of all clones on a two-element set {0, 1}, ordered by inclusion. It is named for Emil Post, who published a complete description of the lattice in 1941. The relative simplicity of Post's lattice is in stark contrast to the lattice of clones on a three-element set, which has the cardinality of the continuum, and a complicated inner structure. A modern exposition of Post's result can be found in Lau (2006).
In Boolean algebra, a parity function is a Boolean function whose value is 1 if and only if the input vector has an odd number of ones. The parity function of two inputs is also known as the XOR function.

In the mathematical field of combinatorics, a bent function is a special type of Boolean function which is maximally non-linear; it is as different as possible from the set of all linear and affine functions when measured by Hamming distance between truth tables. Concretely, this means the maximum correlation between the output of the function and a linear function is minimal. In addition, the derivatives of a bent function are a balanced Boolean functions, so for any change in the input variables there is a 50 percent chance that the output value will change.
In mathematics and optimization, a pseudo-Boolean function is a function of the form
In mathematics and theoretical computer science, analysis of Boolean functions is the study of real-valued functions on or from a spectral perspective. The functions studied are often, but not always, Boolean-valued, making them Boolean functions. The area has found many applications in combinatorics, social choice theory, random graphs, and theoretical computer science, especially in hardness of approximation, property testing, and PAC learning.
Quadratic pseudo-Boolean optimisation (QPBO) is a combinatorial optimization method for quadratic pseudo-Boolean functions in the form



















