Definition
The -variable parity function is the Boolean function with the property that if and only if the number of ones in the vector is odd. In other words, is defined as follows:
where denotes exclusive or.
In Boolean algebra, a parity function is a Boolean function whose value is one if and only if the input vector has an odd number of ones. The parity function of two inputs is also known as the XOR function.
The parity function is notable for its role in theoretical investigation of circuit complexity of Boolean functions.
The output of the parity function is the parity bit.
The -variable parity function is the Boolean function with the property that if and only if the number of ones in the vector is odd. In other words, is defined as follows:
where denotes exclusive or.
Parity only depends on the number of ones and is therefore a symmetric Boolean function.
The n-variable parity function and its negation are the only Boolean functions for which all disjunctive normal forms have the maximal number of 2 n − 1 monomials of length n and all conjunctive normal forms have the maximal number of 2 n − 1 clauses of length n. [1]
Some of the earliest work in computational complexity was 1961 bound of Bella Subbotovskaya showing the size of a Boolean formula computing parity must be at least . This work uses the method of random restrictions. This exponent of has been increased through careful analysis to by Paterson and Zwick (1993) and then to by Håstad (1998). [2]
In the early 1980s, Merrick Furst, James Saxe and Michael Sipser [3] and independently Miklós Ajtai [4] established super-polynomial lower bounds on the size of constant-depth Boolean circuits for the parity function, i.e., they showed that polynomial-size constant-depth circuits cannot compute the parity function. Similar results were also established for the majority, multiplication and transitive closure functions, by reduction from the parity function. [3]
Håstad (1987) established tight exponential lower bounds on the size of constant-depth Boolean circuits for the parity function. Håstad's Switching Lemma is the key technical tool used for these lower bounds and Johan Håstad was awarded the Gödel Prize for this work in 1994. The precise result is that depth-k circuits with AND, OR, and NOT gates require size to compute the parity function. This is asymptotically almost optimal as there are depth-k circuits computing parity which have size .
An infinite parity function is a function mapping every infinite binary string to 0 or 1, having the following property: if and are infinite binary strings differing only on finite number of coordinates then if and only if and differ on even number of coordinates.
Assuming axiom of choice it can be proved that parity functions exist and there are many of them; as many as the number of all functions from to . It is enough to take one representative per equivalence class of relation defined as follows: if and differ at finite number of coordinates. Having such representatives, we can map all of them to ; the rest of values are deducted unambiguously.
Another construction of an infinite parity function can be done using a non-principal ultrafilter on . The existence of non-principal ultrafilters on follows from – and is strictly weaker than – the axiom of choice. For any we consider the set . The infinite parity function is defined by mapping to if and only if is an element of the ultrafilter.
It is necessary to assume at least some amount of choice to prove that infinite parity functions exist. If is an infinite parity function and we consider the inverse image as a subset of the Cantor space , then is a non-measurable set and does not have the property of Baire. Without the axiom of choice, it is consistent (relative to ZF) that all subsets of the Cantor space are measurable and have the property of Baire and thus that no infinite parity function exists; this holds in the Solovay model, for instance.
Related topics:
In the mathematical field of order theory, an ultrafilter on a given partially ordered set is a certain subset of namely a maximal filter on that is, a proper filter on that cannot be enlarged to a bigger proper filter on
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX. The Stone–Čech compactification βX of a topological space X is the largest, most general compact Hausdorff space "generated" by X, in the sense that any continuous map from X to a compact Hausdorff space factors through βX. If X is a Tychonoff space then the map from X to its image in βX is a homeomorphism, so X can be thought of as a (dense) subspace of βX; every other compact Hausdorff space that densely contains X is a quotient of βX. For general topological spaces X, the map from X to βX need not be injective.
In the mathematical discipline of set theory, forcing is a technique for proving consistency and independence results. Intuitively, forcing can be thought of as a technique to expand the set theoretical universe to a larger universe by introducing a new "generic" object .

Kőnig's lemma or Kőnig's infinity lemma is a theorem in graph theory due to the Hungarian mathematician Dénes Kőnig who published it in 1927. It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic, especially in computability theory. This theorem also has important roles in constructive mathematics and proof theory.
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since become fundamental concepts in many branches of mathematics and physics, such as string theory, Chern–Simons theory, knot theory, and Gromov–Witten invariants. Chern classes were introduced by Shiing-Shen Chern.

In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.

In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set that represents the result of the operation or by using transfinite recursion. Cantor normal form provides a standardized way of writing ordinals. In addition to these usual ordinal operations, there are also the "natural" arithmetic of ordinals and the nimber operations.
In abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation , a unary operation , and the constant , satisfying certain axioms. MV-algebras are the algebraic semantics of Łukasiewicz logic; the letters MV refer to the many-valued logic of Łukasiewicz. MV-algebras coincide with the class of bounded commutative BCK algebras.
Harmonic balance is a method used to calculate the steady-state response of nonlinear differential equations, and is mostly applied to nonlinear electrical circuits. It is a frequency domain method for calculating the steady state, as opposed to the various time-domain steady-state methods. The name "harmonic balance" is descriptive of the method, which starts with Kirchhoff's Current Law written in the frequency domain and a chosen number of harmonics. A sinusoidal signal applied to a nonlinear component in a system will generate harmonics of the fundamental frequency. Effectively the method assumes a linear combination of sinusoids can represent the solution, then balances current and voltage sinusoids to satisfy Kirchhoff's law. The method is commonly used to simulate circuits which include nonlinear elements, and is most applicable to systems with feedback in which limit cycles occur.
Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "" and "" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.
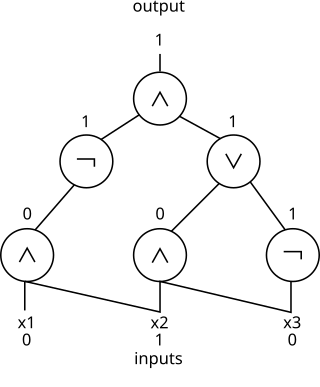
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the circuit complexity of a recursive language that is decided by a uniform family of circuits .
In mathematics, a symmetric Boolean function is a Boolean function whose value does not depend on the order of its input bits, i.e., it depends only on the number of ones in the input. For this reason they are also known as Boolean counting functions.

In computational complexity theory, the decision tree model is the model of computation in which an algorithm can be considered to be a decision tree, i.e. a sequence of queries or tests that are done adaptively, so the outcome of previous tests can influence the tests performed next.
In computational complexity theory, Håstad's switching lemma is a key tool for proving lower bounds on the size of constant-depth Boolean circuits. It was first introduced by Johan Håstad to prove that AC0 Boolean circuits of depth k require size to compute the parity function on bits. He was later awarded the Gödel Prize for this work in 1994.
In mathematics, a submodular set function is a set function that, informally, describes the relationship between a set of inputs and an output, where adding more of one input has a decreasing additional benefit. The natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory and electrical networks. Recently, submodular functions have also found utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains.

Bella Abramovna Subbotovskaya was a Soviet mathematician who founded the short-lived Jewish People's University (1978–1983) in Moscow. The school's purpose was to offer free education to those affected by structured anti-Semitism within the Soviet educational system. Its existence was outside Soviet authority and it was investigated by the KGB. Subbotovskaya herself was interrogated a number of times by the KGB and shortly thereafter was hit by a truck and died, in what has been speculated was an assassination.
In financial mathematics and stochastic optimization, the concept of risk measure is used to quantify the risk involved in a random outcome or risk position. Many risk measures have hitherto been proposed, each having certain characteristics. The entropic value at risk (EVaR) is a coherent risk measure introduced by Ahmadi-Javid, which is an upper bound for the value at risk (VaR) and the conditional value at risk (CVaR), obtained from the Chernoff inequality. The EVaR can also be represented by using the concept of relative entropy. Because of its connection with the VaR and the relative entropy, this risk measure is called "entropic value at risk". The EVaR was developed to tackle some computational inefficiencies of the CVaR. Getting inspiration from the dual representation of the EVaR, Ahmadi-Javid developed a wide class of coherent risk measures, called g-entropic risk measures. Both the CVaR and the EVaR are members of this class.
In mathematics and theoretical computer science, analysis of Boolean functions is the study of real-valued functions on or from a spectral perspective. The functions studied are often, but not always, Boolean-valued, making them Boolean functions. The area has found many applications in combinatorics, social choice theory, random graphs, and theoretical computer science, especially in hardness of approximation, property testing, and PAC learning.

In the mathematical field of set theory, an ultrafilter on a set is a maximal filter on the set In other words, it is a collection of subsets of that satisfies the definition of a filter on and that is maximal with respect to inclusion, in the sense that there does not exist a strictly larger collection of subsets of that is also a filter. Equivalently, an ultrafilter on the set can also be characterized as a filter on with the property that for every subset of either or its complement belongs to the ultrafilter.