
In mathematics, a set B of vectors in a vector space V is called a basis if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.
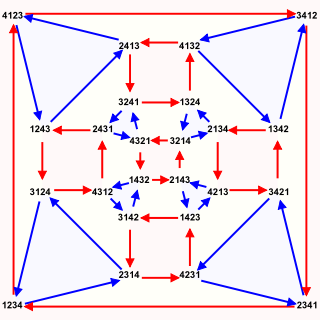
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .
In mathematics, when X is a finite set with at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations. If any total ordering of X is fixed, the parity of a permutation of X can be defined as the parity of the number of inversions for σ, i.e., of pairs of elements x, y of X such that x < y and σ(x) > σ(y).
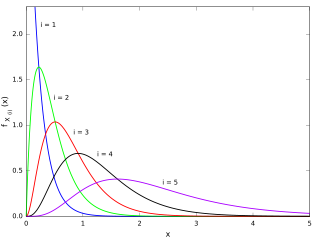
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.
The Fock space is an algebraic construction used in quantum mechanics to construct the quantum states space of a variable or unknown number of identical particles from a single particle Hilbert space H. It is named after V. A. Fock who first introduced it in his 1932 paper "Konfigurationsraum und zweite Quantelung".

Vapnik–Chervonenkis theory was developed during 1960–1990 by Vladimir Vapnik and Alexey Chervonenkis. The theory is a form of computational learning theory, which attempts to explain the learning process from a statistical point of view.
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity. This ring serves as universal structure in which relations between symmetric polynomials can be expressed in a way independent of the number n of indeterminates. Among other things, this ring plays an important role in the representation theory of the symmetric group.

In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.

In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series. They are named for the parity of the powers of the power functions which satisfy each condition: the function is an even function if n is an even integer, and it is an odd function if n is an odd integer.
In mathematics, a symmetric polynomial is a polynomial P(X1, X2, …, Xn) in n variables, such that if any of the variables are interchanged, one obtains the same polynomial. Formally, P is a symmetric polynomial if for any permutation σ of the subscripts 1, 2, ..., n one has P(Xσ , Xσ , …, Xσ ) = P(X1, X2, …, Xn).
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial can be expressed as a polynomial in elementary symmetric polynomials. That is, any symmetric polynomial P is given by an expression involving only additions and multiplication of constants and elementary symmetric polynomials. There is one elementary symmetric polynomial of degree d in n variables for each nonnegative integer d ≤ n, and it is formed by adding together all distinct products of d distinct variables.
In mathematics, Newton's identities, also known as the Girard–Newton formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monic polynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, including general relativity.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of polynomial irreducible representations of the general linear groups. The Schur polynomials form a linear basis for the space of all symmetric polynomials. Any product of Schur polynomials can be written as a linear combination of Schur polynomials with non-negative integral coefficients; the values of these coefficients is given combinatorially by the Littlewood–Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials.
In combinatorial mathematics a cycle index is a polynomial in several variables which is structured in such a way that information about how a group of permutations acts on a set can be simply read off from the coefficients and exponents. This compact way of storing information in an algebraic form is frequently used in combinatorial enumeration.
In mathematics, symmetrization is a process that converts any function in variables to a symmetric function in variables. Similarly, antisymmetrization converts any function in variables into an antisymmetric function.
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials. Every symmetric polynomial can be expressed as a polynomial expression in complete homogeneous symmetric polynomials.
In quantum mechanics, an antisymmetrizer is a linear operator that makes a wave function of N identical fermions antisymmetric under the exchange of the coordinates of any pair of fermions. After application of the wave function satisfies the Pauli exclusion principle. Since is a projection operator, application of the antisymmetrizer to a wave function that is already totally antisymmetric has no effect, acting as the identity operator.
In algebra and in particular in algebraic combinatorics, a quasisymmetric function is any element in the ring of quasisymmetric functions which is in turn a subring of the formal power series ring with a countable number of variables. This ring generalizes the ring of symmetric functions. This ring can be realized as a specific limit of the rings of quasisymmetric polynomials in n variables, as n goes to infinity. This ring serves as universal structure in which relations between quasisymmetric polynomials can be expressed in a way independent of the number n of variables.
Plethystic substitution is a shorthand notation for a common kind of substitution in the algebra of symmetric functions and that of symmetric polynomials. It is essentially basic substitution of variables, but allows for a change in the number of variables used.































