
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix.
In mathematics, the tensor product of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted .
In linear algebra, the outer product of two coordinate vectors is the matrix whose entries are all products of an element in the first vector with an element in the second vector. If the two coordinate vectors have dimensions n and m, then their outer product is an n × m matrix. More generally, given two tensors, their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra.
In mathematics, especially the usage of linear algebra in mathematical physics and differential geometry, Einstein notation is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the canonical pairing of a vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor(s) caused by applying the summation convention to a pair of dummy indices that are bound to each other in an expression. The contraction of a single mixed tensor occurs when a pair of literal indices of the tensor are set equal to each other and summed over. In Einstein notation this summation is built into the notation. The result is another tensor with order reduced by 2.

In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. Briefly, a contravariant vector is a list of numbers that transforms oppositely to a change of basis, and a covariant vector is a list of numbers that transforms in the same way. Contravariant vectors are often just called vectors and covariant vectors are called covectors or dual vectors. The terms covariant and contravariant were introduced by James Joseph Sylvester in 1851.

In mathematics, the exterior algebra or Grassmann algebra of a vector space is an associative algebra that contains which has a product, called exterior product or wedge product and denoted with , such that for every vector in The exterior algebra is named after Hermann Grassmann, and the names of the product come from the "wedge" symbol and the fact that the product of two elements of is "outside"

In physics, Minkowski space is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
Multilinear algebra is the study of functions with multiple vector-valued arguments, with the functions being linear maps with respect to each argument. It involves concepts such as matrices, tensors, multivectors, systems of linear equations, higher-dimensional spaces, determinants, inner and outer products, and dual spaces. It is a mathematical tool used in engineering, machine learning, physics, and mathematics.
In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multilinear concept. Their properties can be derived from their definitions, as linear maps or more generally; and the rules for manipulations of tensors arise as an extension of linear algebra to multilinear algebra.
In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space or of the physical space. Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in material object, and in numerous applications in the physical sciences. As a tensor is a generalization of a scalar and a vector, a tensor field is a generalization of a scalar field and a vector field that assigns, respectively, a scalar or vector to each point of space. If a tensor A is defined on a vector fields set X(M) over a module M, we call A a tensor field on M. Many mathematical structures called "tensors" are also tensor fields. For example, the Riemann curvature tensor is a tensor field as it associates a tensor to each point of a Riemannian manifold, which is a topological space.
In mathematics and theoretical physics, a tensor is antisymmetric onan index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. The index subset must generally either be all covariant or all contravariant.
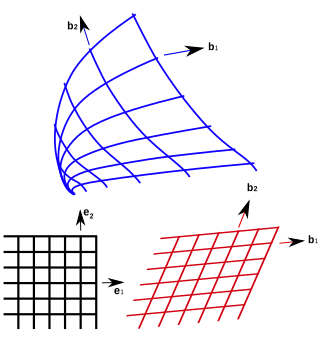
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any basis and, in particular, are non-numerical. Thus it should not be confused with the Ricci calculus. The notation was introduced by Roger Penrose as a way to use the formal aspects of the Einstein summation convention to compensate for the difficulty in describing contractions and covariant differentiation in modern abstract tensor notation, while preserving the explicit covariance of the expressions involved.
When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
In mathematics, a metric connection is a connection in a vector bundle E equipped with a bundle metric; that is, a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve. This is equivalent to:
The mathematics of general relativity is complicated. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.
In mathematics, a symmetric tensor is a tensor that is invariant under a permutation of its vector arguments:
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern name for what used to be called the absolute differential calculus, developed by Gregorio Ricci-Curbastro in 1887–1896, and subsequently popularized in a paper written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century.







